ЛАБОРАТОРНАЯ РАБОТА № 4

Маховое колесо

Цель работы: определить момент инерции махового колеса и момент сил трения.

Приборы и принадлежности: маховое колесо, секундомер, штангенциркуль, линейка, угольник.

Маховое колесо представляет собой массивное тело, вращающееся на подшипниках вокруг горизонтальной оси. На вал колеса радиуса r наматывается нить с подвешенным грузом массы m (рис. 16).

Опускаясь с некоторой высоты h₁, груз раскручивает колесо и, достигнув нижней точки, начинает подниматься вверх за счет запасенной кинетической энергии колеса. При отсутствии сил сопротивления высота подъема груза h₂ была бы равна h₁ в соответствии с законом сохранения механической энергии. В действительности же, ввиду действия сил трения в подшипниках, сопротивления воздуха, а также выделения тепла в нити, груз поднимается на несколько меньшую высоту. В рассматриваемом случае главной причиной потерь энергии является действие сил трения.

Известно, что если в замкнутой системе действуют неконсервативные силы (например, силы трения), то работа этих сил равна изменению полной механической энергии системы:

DE = E₂ - E₁ = A_тр.

Рассмотрим систему колесо-груз в крайних положениях h₁ и h₂, когда кинетическая энергия равна нулю, т.е. механическая энергия системы равна потенциальной энергии груза.

Тогда

DE = E₂ - E₁ = mgh₂ - mgh₁ = A_тр = -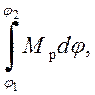

где М_тр - модуль момента сил трения. Знак «минус» в правой части указывает на то, что работа сил трения отрицательна. Интеграл берется в пределах полного угла поворота колеса при опускании и подъеме груза.

Момент сил трения можно считать практически не зависящим от скорости вращения, т.е. постоянной величиной. Следовательно.

А_{т р}= - М_тр Dj.

Пусть h₁ и h₂ отсчитываются от нижнего положения груза. Груз при движении проходит расстояние h₁+h₂, а колесо поворачивается на угол

В результате

Рис. 16

На колесо действуют только две силы с отличными от нуля моментами – сила натяжения нити Т и сила трения (рис.16). Поэтому закон движения SМ_I = Je, запишется в виде:

T×r - M_тр = Je,

где e - угловое ускорение колеса.

Второй закон Ньютона для груза:

mg – T = ma,

где а – ускорение груза.

Учитывая, что тангенциальное ускорение точек обода вала равно ускорению груза (нить нерастяжима) а = а_t,

а = er.

Так как сила трения постоянна, то ускорение постоянно, т.е. применимо уравнение равноускоренного движения

где t₁ – время опускания груза.

Окончательно

где d = 2r – диаметр вала.

Измерения

1. Измерить диаметр вала колеса и диаметр нити. Найдите их сумму d.

2. Поднимая груз на одинаковую высоту h₁, несколько раз измерить время опускания груза t₁ и высоту подъема h_2.

Результаты измерений занести в таблицу.

Таблица

Оценить ошибки прямых измерений.

Записать окончательные результаты в виде

J=<J> + S_I,

M_тр=<М_тр > + S_M.

Контрольные вопросы

1. Проанализировать полученные результаты.

2. Что называется моментом силы, моментом инерции и угловым ускорением?

3. Основной закон динамики вращательного движения.

4. Вывести расчетные формулы. Какие упрощающие предположения сделаны при их выводе?

5. Оценить потери энергии в нити и сравнить с потерями в подшипниках.

6. Найти основные источники погрешностей. Предложить методы их уменьшения.

ЛАБОРАТОРНАЯ РАБОТА №5

Колебания маятников

Цель работы: изучить колебания математического и физического маятника. Определить ускорение свободного падения из периода колебаний математического, физического и оборотного маятников.

Приборы и материалы: Оборотный маятник, секундомер, линейка, установка ELWRO.

Упражнение 1. Математический маятник.

В физике маятником называют твердое тело, которое может совершать под действием силы тяжести колебания относительно неподвижной горизонтальной оси. Простейшим маятником является математический – массивное тело исчезающих малых размеров, подвешенное на тонкой нерастяжимой нити.

Движение мятника можно охарактеризовать углом отклонения от вертикали. Тогда как и в случае вращательного движения

где J – момент инерции, М – вращающий момент – момент силы тяжести.

Момент инерции шарика, подвешенного на нити относительно точки название 0 при условии пренебрежения массой нити.

J =

Если радиус r мал, по сравнению с длиной нити a, тогда можно считать, что:

J = ma

Момент силы -

M= mg a sin 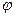= mg a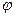

Это дает уравнение колебаний маятника:

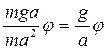
и период колебаний маятника

T = 2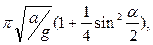

a – угол отклонения маятника.

1. Включить установку и прогреть ее в течение 5-10 минут. Прежде чем выполнять работу необходимо определить диапазон, изохронности колебаний. Отклонив мятник на расстояние 3 см от положения равновесия (при длине мятника 50 см) нажать кнопку «пуск» и отпустить маятник. Прибор автоматически начинает отсчет числа колебаний и времени при прохождении шариком положения равновесия. При появлении отсчета числа колебании 29 нажать кнопку «стоп». Отсчет прекратится при 30 колебаниях.

Повторить измерения для 5,7,10,15 см. Построить график зависимости периода колебаний от начальной амплитуды.

2. Изменяя длину маятника каждый раз на 5см, измерить период колебаний в зависимости от длины. Построить график зависимости Т от . При измерениях амплитуды выбирать в соответствии с первым пунктом работы, так чтобы отклонение периода колебаний от среднего не превышало 0,5%.

3. Определить ускорение свободного падения.

Не нашли, что искали? Воспользуйтесь поиском: