
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Компоненты изменения численности населения России, 1960-2000 гг.

Среднее население
Абсолютная численность населения, о которой шла речь выше, является моментным показателем. Она или исчисляется на дату переписи, или рассчитывается с помощью уравнения демографического баланса по состоянию на 1 января или любую другую дату года. Между тем демографические события - рождения, смерти, браки, разводы, прибытия и отбытия - происходят на протяжении того или иного периода времени.. Длина этого периода может быть разной, но демография чаще всего оперирует периодами, длина которых равна 1 году.
Все статистические показатели перечисленных демографических процессов относятся к периоду, или, говоря строго, являются периодическими. Отсюда возникает проблема сопоставимости периодических данных о демографических процессах с моментными данными о численности населения. К тому же численность населения в начале периода и в его конце оказывается различной, поскольку население меняется непрерывно. Сказанное делает необходимым решение данной проблемы, что может быть достигнуто превращением периодического показателя в моментный с помощью сокращения длины интервала времени, для которого фиксируются демографические события. Если предположить, что этот интервал обращается в нуль, то мы получаем показатель, который называется силой демографического процесса.
Другим способом решения названной выше проблемы является обращение моментного показателя численности населения в периодический. Это достигается с помощью усреднения численности населения, т.е. расчета показателя, характеризующего население не на какой-то момент времени, а за период в целом.
Этим показателем является показатель числа человеко-лет, прожитых населением за период, или его приближение, называемое средним населением.
Показатель числа человеко-лет, прожитых населением за период, позволяет точнее учесть тот очевидный факт, что разные люди в пределах одного и того же периода времени проживают разные его доли. Поэтому они вносят разный вклад в изменения численности населения и в различной степени подвержены риску наступления тех или иных демографических событий в течение этого периода. Часть людей проводит в данном населении весь расчетный период от его начала до его конца, другие же могут или умереть в тот или иной момент внутри данного периода, или уехать, или же, наоборот, родиться или приехать. Некоторые из родившихся внутри периода не доживут до его конца. А кто-то может уехать, а потом вернуться, или, наоборот, приехать, а затем покинуть данное население. И причем не один раз.
Словом, каждый человек из данного населения может прожить в нем или весь период времени, или какую-то его часть (долю). И это определяет тот индивидуальный вклад, который каждый вносит в общие изменения численности населения, в подверженность риску наступления тех или иных демографических событий. Чтобы учесть эти различия, и рассчитывают показатель общего числа прожитых человеко-лет.
Для этого просто суммируют части того периода времени, для которого выполняются демографические расчеты, прожитые в течение этого периода каждым человеком. При этом те, кто прожил весь этот период времени, берутся с весом, равным 1, остальные же - с весом, равным прожитой ими части (доли) этого периода. В табл. 3.2 приведен условный пример такого расчета общего числа человеко-лет, прожитых в течение года населением маленького города.
Таблица 3.2
Расчет числа человеко-лет, прожитых населением условного города1
| Количество человек | События и даты | Число прожитых дней | Число прожитых человеко-лет | |
| Население на 1 января | ||||
| Проживало в городе постоянно с 01.01 по 31. 12 | ||||
| Родился 11 января | 0,97 | |||
| Родился 11 января | Умер 9 ноября | 0,83 | ||
| Умерли 15 января | 8,22 | |||
| Родился 21 февраля | Умер 23 апреля | 0,18 | ||
| 1 2 | Родился 6 марта | Умер 31 марта Умерли 8 апреля | 25 196 | 0,07 0,54 |
| Родились 10 апреля | 68,25 | |||
| Прибыли в город из другого места 18 апреля | 2,83 | |||
| Умер 1 июня | 0,42 | |||
| Умер 5 июня | 0,43 | |||
| Родился 7 июня | 0,57 | |||
| Умер 22 июня | 0,47 | |||
| Родился 24 июня | 0,52 | |||
| Умер 30 июня | 0,5 | |||
| Выехал из города 16 августа | 0,62 | |||
| Родился 26 августа | 0,35 | |||
| Родился 13 сентября | Умер 13 ноября | 0,17 | ||
| Родился 1 октября | 0,25 | |||
| Родились 7 октября | 0,46 | |||
| Родились 19 октября | 0,4 | |||
| Прибыли в город из другого места 25 октября | 18,36 | |||
| Всего прожито человеко-лет | 598,41 | |||
| Население на 31 декабря |
Такого рода расчеты возможно выполнять лишь для небольших населений (как в приведенном в табл. 3.2 примере) и лишь при условии хорошо налаженного учета естественного движения и миграции. Для больших населений такие расчеты делать затруднительно (хотя и возможно). Поэтому на практике обычно ограничиваются расчетом показателей, которые являются приближениями общего числа человеко-лет и которые называются общим именем среднее население.
Одним из таких показателей является население на середину периода, которое является хорошим приближением общего число прожитых человеко-лет. Данный показатель обычно используют для периодов, равных одному году, если есть хорошо налаженная помесячная статистика демографических событий и отсутствуют резкие скачки в численности населения внутри расчетного периода.
Другие показатели основаны на использовании того или иного метода расчета средней хронологической. Применение конкретного метода расчета средней хронологической зависит от того, какая математическая модель изменения численности населения внутри периода принимается. Обычно считается, что население меняется или равномерно (линейно, в арифметической прогрессии)*, или с постоянным темпом (экспоненциально, в геометрической прогрессии).
Если принимается гипотеза равномерного изменения, т.е. если полагают, что население за одинаковые промежутки времени изменяется (растет или убывает) на одну и ту же величину, то среднее население рассчитывается как полусумма численностей населения на начало и конец периода:
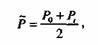 (3.1)
(3.1)
где Р - среднее население; Р0 и Рt, - соответственно население на начало и конец периода.
Кстати, использование показателя население на середину периода основано как раз на предположении о том, что численность населения меняется линейно. При этом чем короче период времени, тем более точным приближением общего числа прожитых человеко-лет является население на середину периода. Поэтому обычно этот показатель используют только для периодов длиною в один год.
Данный показатель тем точнее, чем ближе гипотеза равномерности (линейности) к реальности. Приведем пример расчета среднего населения по формуле (3.1), используя данные об изменении численности населения России в 90-е гг. (См.: Приложение 3).
Население России на 01.01.1990 г. - 148 040,7 тыс. человек. Население России на 01.01.2000 г. - 145 524,8 тыс. человек.
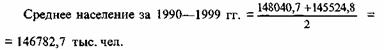
Формула (3.1) существует также в несколько ином, но полностью математически тождественном виде:

Однако гипотеза равномерного (линейного, в арифметической прогрессии) изменения для больших периодов времени является слишком сильным и далеким от реальности предположением, а потому практически неприменима. Поэтому формула (3.1) применяется только для периодов, равных одному году. В этом случае среднее население называется среднегодовым населением.
Если речь идет о более длительных периодах времени, то от этой гипотезы приходится отказываться и использовать для расчета среднего населения другие методы.
В частности, если известны данные не только на конечные, но и на промежуточные даты, то хронологическая средняя может быть рассчитана как взвешенная арифметическая из всех имеющихся численностей, при этом численности на начало и конец периода берутся с весом 1/2, а все прочие - с весом 1:
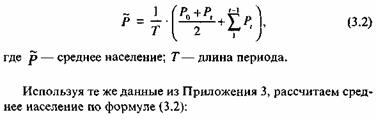

Как видим, среднее население, рассчитанное по этой формуле оказалось на 1041,5 тыс. человек больше, чем то, которое дал расчет по формуле (3.1). Это произошло из-за того, что население России в этот период изменялось отнюдь не равномерно.
Однако и внутри календарного года возможны ситуации, когда гипотеза равномерности не работает (например, в курортных городах) и среднегодовое население не может служить приближением общего числа прожитых человеко-лет. Кстати, и примере, приведенном в табл. 3.2, среднегодовое население
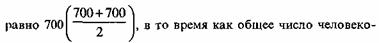
лет - всего лишь 598,41 человека. В таких случаях, чтобы избежать ошибок при расчете демографических показателей, целесообразно применять формулу (3.2), если, конечно, известны данные о численности населения на промежуточные даты.
Для длительных периодов времени, когда гипотеза равномерности не работает, необходимо применять гипотезу изменения численности населения с постоянным темпом (экспоненциально, в геометрической прогрессии). Этот случай обсуждается ниже в этой главе (§3.2.2), где речь идет о непрерывном тем-

Как видим, расчет по формуле (3.3), т.е. в соответствии с гипотезой экспоненциального изменения численности населения, дал ее среднюю величину за период 1990-2000 гг. меньшую, чем по формулам (3.1) и (3.2).
Не нашли, что искали? Воспользуйтесь поиском: