
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Предел функции. Дифференциальное исчисление функции одной переменной.
Семестровая работа №2.
1. Вычислить пределы.
Вариант 1
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 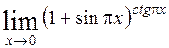
9)  ; 10)
; 10)  .
.
Вариант 2
1) 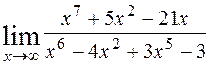 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ;
;
10)  .
.
Вариант 3
1)  ; 2)
; 2)  ; 3)
; 3) 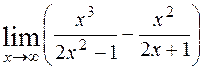 ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 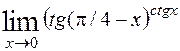
9)  ; 10)
; 10)  .
.
Вариант 4
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 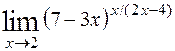
9)  ; 10)
; 10)  .
.
Вариант 5
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 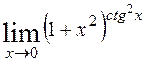
9)  ; 10)
; 10)  .
.
Вариант 6
1)  ; 2)
; 2)  ; 3)
; 3) 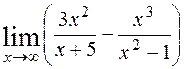 ; 4)
; 4)  ; 5)
; 5) 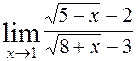 ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 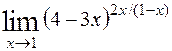
9)  ; 10)
; 10) 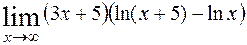 .
.
Вариант 7
1) 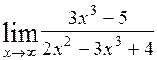 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10) 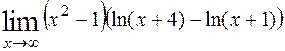 .
.
Вариант 8
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 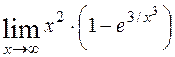
9)  ; 10)
; 10)  .
.
Вариант 9
1)  ; 2)
; 2) 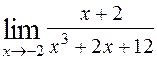 ; 3)
; 3) 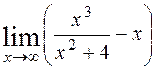 ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 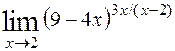
9)  ; 10)
; 10) 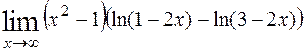 .
.
Вариант 10
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 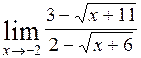 ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 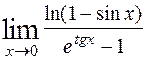
9)  ; 10)
; 10)  .
.
Вариант 11
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 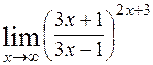
9)  ; 10)
; 10)  .
.
Вариант 12
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 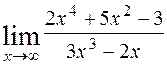 ; 5)
; 5) 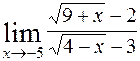 ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 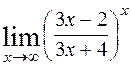
9) 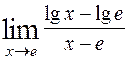 ; 10)
; 10)  .
.
Вариант 13
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 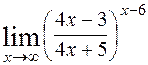
9)  ; 10)
; 10)  .
.
Вариант 14
1) 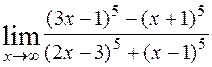 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 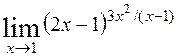
9)  ; 10)
; 10)  .
.
Вариант 15
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7) 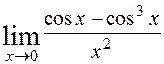 ; 8)
; 8) 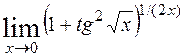
9)  ; 10)
; 10)  .
.
Вариант 16
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9) 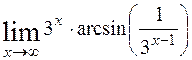 ; 10)
; 10)  .
.
Вариант 17
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6) 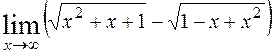 ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  .
.
Вариант 18
1) 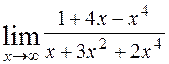 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 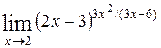
9)  ; 10)
; 10)  .
.
Вариант 19
1)  ; 2)
; 2) 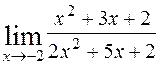 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7) 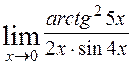 ; 8)
; 8) 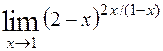
9)  ; 10)
; 10)  .
.
Вариант 20
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7) 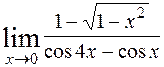 ; 8)
; 8) 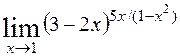
9) 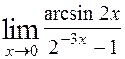 ; 10)
; 10)  .
.
Вариант 21
1) 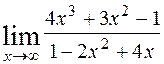 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 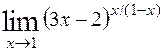 ; 9)
; 9)  ; 10)
; 10)  .
.
Вариант 22
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  .
.
Вариант 23
1) 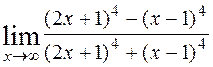 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8) 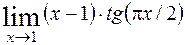 ;
;
9) 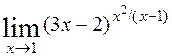 ; 10)
; 10)  .
.
Вариант 24
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  .
.
Вариант 25
1) 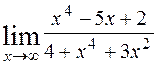 ; 2)
; 2) 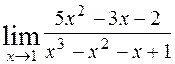 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  .
.
Вариант 26
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  .
.
Вариант 27
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  .
.
Вариант 28
1)  ; 2)
; 2)  ; 3)
; 3) 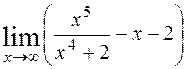 ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  .
.
Вариант 29
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  .
.
Вариант 30
1)  ; 2)
; 2) 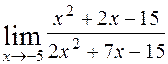 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  ;
;
6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ;
;
10)  .
.
2. Показать, что функции f (x) и g(x) являются бесконечно малыми или бесконечно большими одного порядка.
1.  при
при 
| 11. 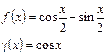 при
при 
| 21.  при
при 
|
2.  при
при 
| 12.  при
при 
| 22.  при
при 
|
3.  при
при 
| 13.  при
при 
| 23.  при
при 
|
4.  при
при 
| 14.  при
при 
| 24.  при
при 
|
5.  при
при 
| 15.  при
при 
| 25.  при
при 
|
6.  при
при 
| 16.  при
при 
| 26. 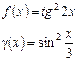 при
при 
|
7.  при
при 
| 17. 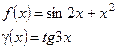 при
при 
| 27.  при
при 
|
8.  при
при 
| 18.  при
при 
| 28.  при
при 
|
9.  при
при 
| 19.  при
при 
| 29.  при
при 
|
10.  при
при 
| 20.  при
при 
| 30.  при
при 
|
3. Задана функция y = f (x). Требуется найти точки разрыва, если они существуют. Сделать чертеж.
1. 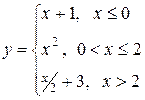
| 11. 
| 21. 
|
2. 
| 12. 
| 22. 
|
3. 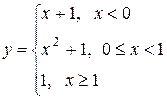
| 13. 
| 23. 
|
4. 
| 14. 
| 24. 
|
5. 
| 15. 
| 25. 
|
6. 
| 16. 
| 26. 
|
7. 
| 17. 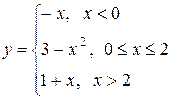
| 27. 
|
8. 
| 18. 
| 28. 
|
9. 
| 19. 
| 29. 
|
10. 
| 20. 
| 30. 
|
4. Задана функция y=f(x) и два значения аргумента x 1 и x 2. Требуется установить, является ли данная функция непрерывной или разрывной для каждого из значений x и найти ее односторонние пределы в этих точках.
1.  ; ;
 ; ;  . .
| 11.  ; ;
 ; ; 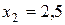
| 21.  ; ;
 ; ; 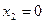 . .
|
2.  ; ;
 ; ; 
| 12.  ; ;
 ; ;  . .
| 22.  ; ;
 ; ; 
|
3.  ; ;
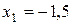 ; ; 
| 13.  ; ;
 ; ; 
| 23.  ; ;
 ; ; 
|
4. 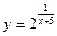 ; ;
 ; ; 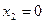 . .
| 14.  ; ;
 ; ;  . .
| 24.  ; ;
 ; ; 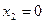 . .
|
5.  ; ;
 ; ;  . .
| 15.  ; ;
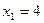 ; ;  . .
| 25.  ; ;
 ; ; 
|
6.  ; ;
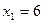 ; ; 
| 16.  ; ;
 ; ; 
| 26.  ; ;
 ; ; 
|
7. 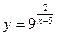 ; ;
 ; ; 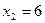
| 17.  ; ;
 ; ;  . .
| 27.  ; ;
 ; ; 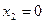 . .
|
8.  ; ;
 ; ;  . .
| 18.  ; ;
 ; ;  . .
| 28.  ; ;
 ; ; 
|
9. 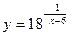 ; ;
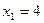 ; ; 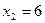
| 19.  ; ;
 ; ;  . .
| 29.  ; ;
 ; ;  . .
|
10.  ; ;
 ; ; 
| 20.  ; ;
 ; ;  . .
| 30.  ; ;
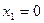 ; ; 
|
5. Составить уравнение нормали и касательной к данной кривой в точке с абсциссой x о.
1. а) y=(4x–x2)/4, xо=2;
б) 
| 11. а) y=x/(x2+1), xо=−2;
б) 
| 21. а) y=x2+8 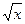 −32, xо=4;
б) −32, xо=4;
б) 
|
2. а) y=x–x3, xо=–1;
б) 
| 12. а) y=2x/(x2+1), xо=1;
б) 
| 22. а) y=  −20, xо=–8;
б) −20, xо=–8;
б) 
|
3. а) y= 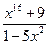 , x0=1;
б) , x0=1;
б) 
| 13. а) y=  , xо=1;
б) , xо=1;
б) 
| 23. а) y=(x3+2)/(x3−2), xо=2;
б) 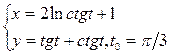
|
4. а) y=  , xо=4;
б) , xо=4;
б) 
| 14. а) y=  , xо=1;
б) , xо=1;
б) 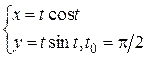
| 24. а) y=  , xо=1;
б) , xо=1;
б) 
|
5. а) y=2x2–3x+1, xо=1;
б) 
| 15. а) y=  /10+3, xо=2;
б) /10+3, xо=2;
б) 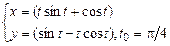
| 25. а) y=( −2x−3)/4, xо=4;
б) −2x−3)/4, xо=4;
б) 
|
6. а) y= 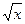 −3 −3  , xо=64;
б) , xо=64;
б) 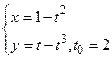
| 16. а) y=6  , xо=1;
б) , xо=1;
б) 
| 26. а) y=(3x−2 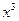 )/3, xо=1;
б) )/3, xо=1;
б) 
|
7. а) y=x+  , xо=1;
б) , xо=1;
б) 
| 17. а) y=2x2+3x–1, xо=–2;
б) 
| 27. а) y=4 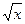 −5 −5  +2, xо=1;
б) +2, xо=1;
б) 
|
8. а) y=2x+1/x, xо=1;
б) 
| 18. а) y=8  −70, xо=16;
б) −70, xо=16;
б) 
| 28. а) y=2( +3 +3 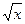 ), xо=1;
б) ), xо=1;
б) 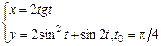
|
9. а) y=3  − − 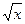 , xо=1;
б) , xо=1;
б) 
| 19. а) y=(x2−3x+6)/x2, xо=3;
б) 
| 29. а) y=(x2−3x+3)/3, xо=3;
б) 
|
10. а) y=3( −2 −2 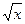 ), xо=1;
б) ), xо=1;
б) 
| 20. а) y=1/(3x+2), xо=2;
б) 
| 30. а) y=3(x4+1)/ 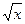 , xо=1.
б) , xо=1.
б) 
|
6. Найти дифференциал функции d y.
1. а)  ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
| 16. а)y=  .
б) y= .
б) y=  ,
в) y=ln ,
в) y=ln  . .
|
2. а)  ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 17. а)  ,
б) y= ,
б) y=  ,
в) y=2 ,
в) y=2  . .
|
3. а)  ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 18. а)y=  ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
|
4. а)  ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 19. а) y=arctg  ,
б) y= ,
б) y= 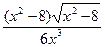 ,
в) y= x (cos(ln x)+sin(ln x))/2. ,
в) y= x (cos(ln x)+sin(ln x))/2.
|
5. а)  ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
| 20. а) 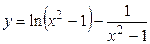 ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
|
6. а) y= 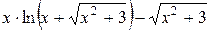 ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 21. а) y =arctg  ,
б) y= ,
б) y= 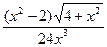 ,
в) y=lntg ,
в) y=lntg  . .
|
7. а)  ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 22. а) y=ln  ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
|
8. а)  ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
| 23 а) y=ln  ×tg ×tg 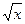 ,
б) y= ,
б) y=  ,
в) y=lnsin ,
в) y=lnsin  . .
|
9. а) y=ln  ,
б) y= ,
б) y= 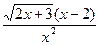 ,
в) y=ln(arccos ,
в) y=ln(arccos  ). ).
| 24. а) y=  ,
б) y= ,
б) y=  ,
в) y=lg(ln(ctgx)). ,
в) y=lg(ln(ctgx)).
|
10. а)  ,
б) y= ,
б) y=  ,
в) y= ,
в) y= 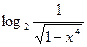 . .
| 25. а) y= x ×(sin(ln x)–cos(ln x)),
б) y=  ,
в) ,
в)  . .
|
11. а) y=    ,
б) y= ,
б) y=  ,
в) y=ln(arcsin ,
в) y=ln(arcsin  ). ).
| 26. а) 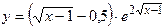 ,
б) y= ,
б) y= 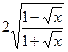 ,
в) y=lncos ,
в) y=lncos  . .
|
12. а) y=ln 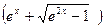 + +  ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 27. а) y =cos x ×lntg x –lntg(х /2),
б) y=  ,
в) y=ln ,
в) y=ln 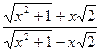 . .
|
13. а)y=  ,
б) y= ,
б) y=  ,
в) ,
в)  . .
| 28. а) y=   ,
б) y= ,
б) y=  ,
в) ,
в)  . .
|
14. а) y=ln(tg(x /2))– x /sin x,
б) y=  ,
в) y=ln ,
в) y=ln  . .
| 29. а) y= 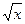 -(1+ x)×arctg -(1+ x)×arctg 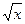 ,
б) y= ,
б) y=  ,
в) y=ln ,
в) y=ln 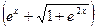 . .
|
15. а)  ,
б) y= ,
б) y=  ,
в) y=ln(ln(sin(1+1/ x))). ,
в) y=ln(ln(sin(1+1/ x))).
| 30. а) y= x ×arctg x –ln  ,
б) y= ,
б) y=  ,
в) y= ,
в) y=  . .
|
7. Найти производную функции.
| <== предыдущая лекция | | | следующая лекция ==> |
| Логико-грамматические «квазипространственные» речевые конструкции | | | Условия и характер труда |
Не нашли, что искали? Воспользуйтесь поиском: