КОНТРОЛЬНОЇ РОБОТИ № 1.

В рекомендованих підручниках [1], [2], а також у керівництвах [4] i [5] студенти знайдуть достатню кількість прикладів та задач, подібних до тих, які включені в контрольну роботу. Тому нижче подані лише необхідні короткі методичні вказівки до рішення задач контрольної роботи.

Першу задачу (задачі 1-10) слід вирішувати після вивчення тем 1.1 та 1.2. У всіх задачах розглядається рівновага плоскої системи сил, що сходяться, та необхідно визначити реакції двох шарнірно з’єднаних між собою стержнів, які підтримують пару

вантажів. Отже, на шарнір В в кожній задачі діють взагалі чотири сили, дві з яких невідомі. Можна вибрати три способи рішення: -

- 11 -

аналітичний, графічний та геометричний. Для даного типу задач доцільніше використати аналітичний спосіб вирішення.

Послідовність рішення задачі:

1. Вибрати тіло (точку), рівновагу якого слід розглянути.

2. Звільнити тіло (шарнір В) від зв’язків та зобразити діючі на нього активні сили та реакції зв’язків. При цьому реакції зв’язків слід направити від шарніру В, оскільки прийнято вважати, що стержні розтягнуто.

3. Вибрати осі координат та скласти рівняння рівноваги, користуючись умовами рівноваги плоскої системи сил,що сходяться: SFix = 0; SFiy = 0. Раціональним вважається такий вибір координатних осей, коли хоча б одна з них співпадає з однією з невідомих реакцій.

4. Визначити реакції стержнів шляхом рішення вказаної системи рівнянь.

5. Перевірити правильність отриманих результатів. При цьому можна використати два способи: 1) аналітичний – шляхом

рішення системи рівнянь рівноваги; 2) графічний – шляхом побудови силового багатокутника.

Приклад 1. Визначити реакції стержнів, які утримують вантажі F₁ = 70кН та F₂ = 100 кН(мал.1,а). Массою стержнів знехтувати.

- 1 –

Мал.1

- 12 -

Р і ш е н н я. 1. Розглянемо рівновагу шарніру В(мал. 1,б),

оскільки саме в ньому перетинаються лінії дії усіх сил системи.

2. Звільняємо шарнір В від зв’язків та зображуємо діючі на

нього активні сили F₁, F₂ та реакції зв’язків N₁ та N₂.

3. Обираємо систему координат так, щоб ось у співпадала з

невідомим зусиллям N₂. Складаємо рівняння рівноваги для системи сил, діючих на шарнір В:

SFix = -N₁ cos45⁰ +F₂ cos30⁰ = 0; (1)

SFiy = N₁ cos45⁰ + N₂ + F₂ cos60⁰ = 0 (2)

4. Визначаємо реакції стержнів N1 та N2, вирішуючи рівняння (1) і (2). З рівняння (1) отримуємо:

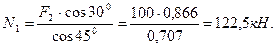
Підставляючи знайдене значення N₁ до рівняння (2), отримуємо:

N₂ = F₁ – F₂ cos60⁰ – N₁ cos45⁰ = 70 – 100 0,5 –

- 122,5 0,707 = - 66,6 кН.

Знак “-“ перед значенням N₂ вказує на те, що спочатку

обраний напрямок реакції невірний – слід спрямувати

реакцію N₂ у протилежному напрямку, тобто до шарніру В (на мал. 1,б дійсний напрямок реакції N₂ показаний штриховим вектором).

6.Перевіряємо правильність отриманих результатів:

а) а н а л і т и ч н и м с п о с о б о м

- обравши новий напрямок координатної осі х₁(мал. 1,б). Складаємо рівняння рівноваги на цю ось(при цьому враховуємо новий напрямок реакції N₂:

SFix₁ = N₁ – F₁ cos45⁰ – N₂ cos45⁰ F₂ cos75⁰ = 122,5 –

- 70 0,707 – 66,6 0,707 – 100 0,258 = 122,5 – 122,5 = 0.

Умова SFix₁ = 0 виконується – отже, реакції N₁ та N₂

знайдені правильно.

- 13 -

Б) г р а ф і ч н и м с п о с о б о м (Мал. 2)

Мал.2

- будуємо силовий багатокутник, враховуючи новий напрямок реакції N₂:

SFi = F₁ + F₂ + N₁ + N₂ = 0

Оскільки силовий багатокутник є замкненим, то система сил знаходиться в рівновазі. Отже, реакції N₁, N₂ знайдені вірно.

Другу задачу (11 – 20) слід вирішувати після вивчення тем 1.3. та 1.4. У всіх задачах потрібно визначити реакції опор балок.

- 14 -

Студентам необхідно отримати навички визначення опор, оскільки

з цього починається рішення багатьох задач з опору матеріалів і деталей машин.

Послідовність рішення задачі:

1. Зобразити балку разом з навантаженням.

2. Вибрати координатні осі так, щоб ось х співпадала з оссю балки, а ось у проходила через лівий край балки.

3. Якщо потрібно, провести необхідні перетворення заданих активних сил:

- силу, нахилену під кутом a замінити двома складовими по осях координат;

- рівномірно розподілене навантаження інтенсивністю q замінити ії рівнодійною Q, яка діє посередині ділянки розподіленого навантаження.

4. Звільнити балку від опор, замінивши їх дію реакціями опор,спрямованними вздовж обраних осей координат.

5. Скласти рівняння рівноваги статики для довільної плоскої системи сил таким чином, щоб рівняння суми моментів були відносно саме тих точок, в яких прикладені невідомі реакції.

6. Перевірити правильність знайдених реакцій за допомогою рівняння, яке не було використано раніше.

Приклад 2. Визначити реакції опор балки. (Мал. 3,а).

Р і ш е н н я.1.Зобразимо розрахункову схему балки:

- усі діючі на неї навантаження;

- обираємо осі координат;

- силу F замінимо на складові:

Fx = Fcosa=20 0,866=17,3кН

Fy =Fcos(90⁰-a)=20 0,5=10кН;

- рівнодійну Q = q CD рівномірно розподіленого навантаження прикладаємо в точці К, посередині ділянки(Мал. 3,б);

- опори у точках A i D замінимо на опорні реакції (Мал.3,в).

2. Складаємо рівняння рівноваги для балки та визначаємо невідомі реакції опор.

З рівняння суми моментів діючих на балку сил відносно однієї з

- 15 -

Мал. 3

опор відразу визначаємо одну з реакцій:

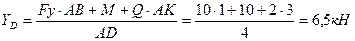
Другу вертикальну реакцію визначаємо з рівняння:

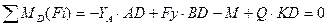, звідки

- 16 -

Визначаємо горизонтальну реакцію:

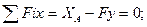звідки .

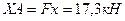3. Перевіримо правильність результатів, користуючись таким рівнянням, яке раніше не застосовували:

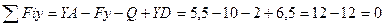
Отже, оскільки умова рівноваги виконується, то реакції опор знайдені вірно.

Третю задачу (задачі 21-30) слід виконувати після вивчення теми 1.5.

Послідовність вирішення задачі:

1. Зобразити розрахункову схему балки, вказавши на ній діючі активні сили, опорні реакції підшипників та осі координат.

2. З умови рівноваги вала, що має нерухому ось, визначити величину сили F₂, потім сили Fr₂.

3. Зпроектувати просторову систему сил на горизонтальну плоскість та визначити горизонтальні складові реакцій підшипників. Перевірити їх правильність.

4. Зпроектувати просторову систему сил на вертикальну плоскість та визначити вертикальні складові реакцій підшипників. Перевірити їх правильність.

Приклад 3. На вал (Мал. 4,а) жорстко насаджені шків 1 та колесо 2. Визначити сили F₂, Fr₂ = 0,4F₂, а також реакції опор підшипників А і В, якщо F₁= 100 Н.

Р і ш е н н я.1.Зображуємо розрахункову схему вала (Мал.4,б)

- 17 -

2. Визначимо F₂, Fr_2. Для цього зпроектуємо вал на плоскість yz, перпендикулярну до осі вала x (Мал. 4, в) і складемо рівняння рівноваги вала відносно цієї осі:

- 17 -

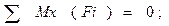
звідки

Мал. 4

3. Визначимо опорні реакції підшипників у горизонтальній плоскості. Для цього зпроектуємо вал на горизонтальну плоскість xy (Мал. 4, г).

Знайдемо горизонтальну реакцію у точці В за допомогою рівняння:

- 18 -

Мал. 4, г

, звідки

.

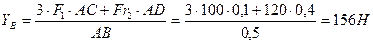Горизонтальна реакція у точці А:

, звідки

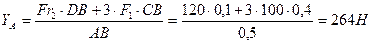
Перевіримо правильність найдених реакцій:

; .

Умова виконується, отже, реакції підшипників у горизонтальній плоскості знайдені вірно.

4. Визначимо опорні реакції підшипників у вертикальній плоскості. Для цього зпроектуємо вал на вертикальну плоскість xz (Мал. 4, д).

- 19 -

Знайдемо вертикальну реакцію у точці В за допомогою

рівняння:

, звідки

Друга вертикальна реакція у точці А:

, звідки

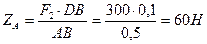
Перевіримо правильність знайдених реакцій:

Умова міцності виконується, отже, реакції підшипників у вертикальній плоскості знайдені вірно.

Четверту задачу (задачі 31-40) слід вирішувати після вивчення тем 1.7, 1.8, 1.9.

Для усіх номерів застосовуються поняття швидкості та прискорення при нерівномірному русі точки.

- 20 -

В усіх задачах розглядається рух точки за траекторією, що складається з прямолінійних ділянок та дуг кіл. Необхідні параметри руху точки визначаються, враховуючи

спосіб завдання руху: S=f(t).

Вид і особливості руху точки визначаються її головними кінематичними характеристиками - дотичним а_t та нормальним а_n прискореннями.

При нерівномірному русі точки

, де - швидкість точки i

r - радіус кривизни траекторії.

В разі прямолінійного руху

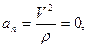оскільки для

прямолінійної траекторії r = ¥

Повне прискорення при цьому дорівнює дотичній складовій: a = а_t.

В разі криволінійного руху

-

- Повне прискорення при цьому буде визначатися як:

При рівномірному русі точки швидкість її є величина постійна:

- а отже, дотична складова прискорення

дорівнює нулю: ,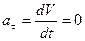

- 21 -

а нормальна складова прискорення буде існувати лише в тому випадку, коли траекторія точки буде криволінійною., тобто радіус кривизни траекторії r = const.

А повне прискорення визначається за формулою:

Приклад 4. Рух автомобіля від положення 0 задано рівняням

S= 0,5 t³ (S - в м t - в с). Траекторію руху автомобіля зображено

на малюнку 4.

Потрібно: 1) побудувати траекторію у масштабі;

2) визначити час, необхідний для переміщення автомобіля в положення 1,2,3;

3) визначити та зобразити на малюнку швидкості та повні прискорення автомобіля в положеннях 1,2,3.

Рішення. Розглядаючи рух автомобіля, можемо його уявити як рух

матеріальної точки, яка має масу та кінематичні характеристики автомобіля. В подальшому під поняттям «точка» маємо на увазі

автомобіль.

1) Зображаємо траекторію точки у масштабі (Мал. 5).

2) Спочатку визначимо час, потрібний для переміщення точки до положень 1,2,3 - відповідно t₁, t₂, t₃.Використовуючи закон руху точки, отримуємо: де S₁ - переміщення точки

від положення 0 до положення 1.

Знайдемо його, використовуючи розмір переміщення:

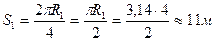
Тоді:

Аналогично знаходимо t₂: де

- 22 -

Nbsp; Мал 5

Тоді:

Знаходимо t₃: де

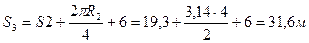
Тоді:

3) Визначимо закон зміни швидкості і прискорення:

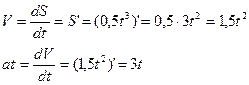
- 23 -

a) для положення 1:

Оскільки положення 1 відповідає кінцевій точці криволінійної

траекторії, то буде існувати нормальна складова прискорення:

Дотична складова:

Повне прискорення точки:

Зображуємо вектори а₁ та V₁ на малюнку (мал. 5).

б) для положення 2:

Оскільки положення 2 знаходиться на криволінійній траекторії, то повне прискорення буде мати дві складові: дотичну і нормальну.

Дотичне прискорення:

Нормальне прискорення:

Повне прискорення точки:

Зображуємо вектори а₂ та V₂ на малюнку(мал. 5).

в) для положення 3:

Оскільки положення 3 знаходиться на прямолінійній траекторії, то повне прискорення буде мати лише одну складову - дотичну.

Дотичне прискорення:

- 24 -

Повне прискорення точки:

Зображуємо вектори а₃ та V₃ на малюнку(мал. 5).

П’ята задача(задачі 41-50) пов’язана з визначенням роботи та потужності або при поступальному, або при обертальному русі.

Задачі слід вирішувати, вивчивши теми 1.14 та 1.15, а також повторивши матеріал про тертя ковзання і тертя кочення. Вирішуючи дані задачі, необхідно уважно стежити за тим, щоб чисельні значення величин були виражені у системі СІ.

У підручниках [1] i [2], а також у керівництві [6] достатньо повно розібрані методи рішення таких задач.

Приведемо лише основні формули, необхідні для обчислення роботи та потужності.

Робота постійної сили F на прямолінійному шляху:

,де a - кут між напрямками

сили та переміщення.

Робота сили тяжіння:

, де Н – різниця рівнів при

переміщенні центру ваги.

Робота пари сил:

, де М – момент пари,

j - кут її повертання.

За СІ робота виражається у джоулях (Дж):

1Дж = 1 Н×м; 1 кДж = 10³ Дж.

Потужність Р визначається за формулою:

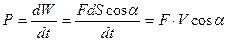, або

при a=0 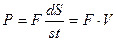, де V – швидкість точки.

При обертальному русі:

- 25 -

або .де М – обертаючий момент,

w - кутова швидкість.

За СІ потужність виражається у ваттах (Вт):

1 Вт = 1 Дж/с 1 кВт = 10³ Вт.

Механічний коефіцієнт корисної дії:

,

де Wп.с. – робота сил корисних опорів;

W - уся робота, яку виконали.

Користуються і такою формулою:

,

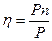де Рп - корисна потужність, Р - уся витрачена потужність.

Не нашли, что искали? Воспользуйтесь поиском: