Интегрирование подстановкой

Учебные и воспитательные цели

1. Изучить методы интегрирования по частям и подстановкой.

2. Развивать математическую интуицию и логическое мышление, воспитывать математическую культуру.

3. Воспитывать у студентов умение применять теоретические знания для решения конкретных практических задач.

I. Учебные вопросы и расчет времени

I. Введениe 5 мин.

II. Основная часть 80 мин.

Учебные вопросы

1. Интегрирование подстановкой 40 мин

2. Интегрирование по частям 40 мин

III. Заключение 5 мин

Введение

Во многих случаях приходится вычислять интегралы, которые нельзя вычислить, пользуясь только таблицей интегралов и свойствами неопределенных интегралов. Для этого разработаны различные методы интегрирования. Одним из самых распространенных методов интегрирования является метод интегрирования по частям и метод замены переменной (или метод подстановки).

Интегрирование подстановкой

Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла, т. е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом интегрирования заменой переменной. Он основан на следующей теореме.

Теорема. Пусть функции f(x) и j(t) определены на некоторых промежутках и имеет смысл сложная функция f[j(t)]. Тогда, если функция y = f(x) имеет первообразную F(x), а функция x = j(t) дифференцируема, то функция f[j(t)]j'(t) также имеет первообразную и справедлива формула

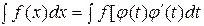(1)

Доказательство: Так как первообразная F(x) определена на том же промежутке, что и функция f(x), и существует сложная функция f[j(t)], то существует и сложная функция. F[j(t)]. Тогда по правилу дифференцирования сложной функции с учетом того, что F'(x) = f(x) получим

(F[j(t)]' = (F[j(t)])'_x·j'(t) = f[j(t)] ·j'(t),

т. е. функция f[j(t)] ·j'(t) имеет в качестве одной из своих первообразных функцию F[j(t)] и, следовательно,

.

Замечаем, что 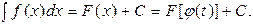Окончательно получим

, т. е. искомую формулу (1).

Формула (1) называется формулой замены переменной в неопределенном интеграле.

Примеры:

1) Вычислить неопределенный интеграл .

Решение. Положим 2х – 3 = t. Следовательно, 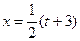. Отсюда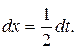

Тогда по формуле (1)

2) Найти неопределенный интеграл

Решение. Положим x –1 = t; x = t + 1. Тогда dx = dt. По формуле (1) получаем

Замечание. При замене переменной в неопределенном интеграле иногда более удобно задавать не х как функциюt, а, наоборот, задавать t как функцию x.

3) При вычислении интегралов вида

полезна подстановка t = j(x).

а)

б)

в)

при n ¹ -1,

=

lnçt ç+ C = ln çsinx ç+ C при n = -1.

Необходимо заметить, что удачный выбор подстановки обычно представляет известные трудности. Для их успешного преодоления необходимо хорошо владеть техникой дифференцирования и твердо знать табличные интегралы.

Не нашли, что искали? Воспользуйтесь поиском: