Типтік есептер шығару үлгілері

Мысал.

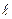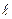Ұзындығы болатын жұқа стерженьда сызықты тығыздығы -ға тең заряд бірқалыпты таралған. А –нүктесіндегі таралған зарядтан пайда болған, стержень осінде (бекітілген) орналастырылған және оның жақын ұшынан -қашықтыққа алыстатылған -потенциалын табу керек.

Шешуі:

Стерженьда ұзындығы кішкене бөлімше белгілейді. Сонда бұл бөлімшеде нүктелік деп санауға болатын 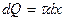заряд анықталынады. А нүктесінде осы нүктелік зарядтан пайда болған 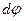потенциалды мына формула бойынша анықтауға болады: Электр өрістерінің суперпозиция принципі бойынша, А-нүктесінде зарядталған стерженьнан пайда болған электр өрісінің потенциалын мына берілгенді интегралдау арқылы табамыз: ; Интегралдау арқылы мынаны аламыз:

; Физикалық шамаларға сандық мәндерін қойып аламыз: (В) Жауабы: 62.4 В

Мысал

Үдеткішті потенциалдар айырымы (U)- ын анықтау керек, онда электр өрісінде электрон жүріп өткен, ол электронның жылдамдығы м/с,

Оның жылдамдығы n=2есе өсу керек.

Шешуі:

Үдеткішті потенциалдар айырымын табу үшін электростатикалық өрістің А күш жұмысын есептеуге болады.

Бұл жұмыс е- элементар зарядтың U- потенциалдар айырымын көбейтіндісі ар/лы анықталынады:

(1)

Бұл жағдайда электростатикалық өрістің күш жұмысы электронның кинетикалық энергиясының өзгерісіне тең:

(2)

мұнда: Т₁және Т₂- электронның кинетикалық энергиясы, m-электрон массасы; және 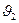- электронның бастапқы және соңғы жылдамдығы.(1)және (2) формулалардың оң бөліктерін теңестіріп, аламыз:

мұнда n=

Потенциалдар айырымы үшін жазамыз:

.

Жауабы: 8,53В

Мысал.

-радиусты жұқа диск -беттік тығыздықпен бірқалыпты зарядталған. Диск осінен -қашықтықта жатқан А нүктесіндегі потенциал мен электр өрісі кернеулігін табу керек.

Шешуі:

А нүктесіндегі потенциалды табу үшін, өрістің суперпозиция принципін пайдалану қолайлы. Ол үшін дискіні қалыңдығы болатын элементар сақиналарға бөлеміз. сақина ауданының радиусының ауданы -қа тең, ал сақина заряды - -қа тең. Сақина өрісінің потенциалы -өзінің нүктелік элементтерінен құралған потенциалдар қосындысына тең.

Нүктелік элементтер А –нүктесінен тең алыстатылғандықтан, сақина зарядын сол шамалас нүктелік зарядпенауыстырсақ, А нүктеден 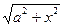қашықтыққа алыстатылғанды мына формуламен табамыз:

;

Сақина потенциалы:

- интегралдап, диск потғенциалын анықтаймыз:

(1)

Симметрия қатысы бойынша мынандай қорытынды жасауға болады, А нүктесінде электр өрісінің кернеулік векторы диск осінің маңына бағытталған. Сондықтан Е –нің модулін табу үшін, электр өрісі кернеулігімен потенциал арасындағы байланысты пайдаланамыз. Мұнда - туынды потенциалдың жылдам өзгерісі бағытында алынып отыр, яғни күштік сызық маңында.

Шаманы айнымалы деп қарастырып, аламыз:

(2)

болғанда, жазылған (2) –формула шексіз жазықтықты өріс кернеулігін есептейтін қорытынды формулаға көшеді:

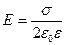
Мысал.

Нүктелік және 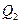- зарядтар бір-бірінен 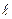- қашықтықта орналасқан. Бұл жүйенің потенциалдық энергиясы қандай?

Шешуі:

Бұл зарядтардың тек әрекеттесіп орналасуы белгілі болса, онда олардың біреуін шартты түрде қозғалмастай етіп бекітілген деп есептеуге болады. Сонда ізделініп отырған энергия -ға тең болады, мұнда өріс потенциалы, ол 2-ші заряд орналасқан нүктедегі 1-ші зарядтан пайда болған.

- екенін ескеріп, жазамыз: ;

Мысал.

Ұзындығы 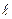болатын жұқа стерженьда сызықты тығыздығы -

ға тең заряд бірқалыпты таралған. А –нүктесіндегі таралған зарядтан пайда болған, стержень осінде (бекітілген) орналастырылған және оның жақын ұшынан 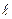-қашықтыққа алыстатылған -потенциалын табу керек.

Шешуі:

Стерженьда ұзындығы кішкене бөлімше белгілейді. Сонда бұл бөлімшеде нүктелік деп санауға болатын 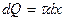заряд анықталынады. А нүктесінде осы нүктелік зарядтан пайда болған 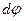потенциалды мына формула бойынша анықтауға болады:

Электр өрістерінің суперпозиция принципі бойынша, А-нүктесінде зарядталған стерженьнан пайда болған электр өрісінің потенциалын мына берілгенді интегралдау арқылы табамыз:

Интегралдау арқылы мынаны аламыз:

;

Физикалық шамаларға сандық мәндерін қойып аламыз:

(В)

Жауабы: 62.4 В

Мысал.

-радиусты жұқа диск -беттік тығыздықпен бірқалыпты зарядталған. Диск осінен -қашықтықта жатқан А нүктесіндегі потенциал мен электр өрісі кернеулігін табу керек.

Шешуі:

А нүктесіндегі потенциалды табу үшін, өрістің суперпозиция принципін пайдалану қолайлы. Ол үшін дискіні қалыңдығы болатын элементар сақиналарға бөлеміз. сақина ауданының радиусының ауданы -қа тең, ал сақина заряды - -қа тең. Сақина өрісінің потенциалы -өзінің нүктелік элементтерінен құралған потенциалдар қосындысына тең.

Нүктелік элементтер А –нүктесінен тең алыстатылғандықтан, сақина зарядын сол шамалас нүктелік зарядпенауыстырсақ, А нүктеден 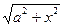қашықтыққа алыстатылғанды мына формуламен табамыз:

;

Сақина потенциалы:

- интегралдап, диск потғенциалын анықтаймыз:

(1)

Симметрия қатысы бойынша мынандай қорытынды жасауға болады, А нүктесінде электр өрісінің кернеулік векторы диск осінің маңына бағытталған. Сондықтан Е –нің модулін табу үшін, электр өрісі кернеулігімен потенциал арасындағы байланысты пайдаланамыз. Мұнда - туынды потенциалдың жылдам өзгерісі бағытында алынып отыр, яғни күштік сызық маңында.

Шаманы айнымалы деп қарастырып, аламыз:

(2)

болғанда, жазылған (2) – формула шексіз жазықтықты өріс кернеулігін есептейтін қорытынды формулаға көшеді:

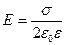
«Электродинамика және салыстырмалылықтың арнайы теориясы »