Ломаная линия, длина ломаной линии, периметр многоугольника

Опираясь на понятие отрезка, учащихся II класса знакомят с ломаной линией. Для этого по образцу, данному учителем, предлагают учащимся построить линию из палочек или бумажных полосок. Учитель дает название новой линии. Можно изготовить также модель ломаной линии, «сломав» на глазах у детей на части тонкую лучинку или кусок проволоки. Так же с опорой на практические работы вводят понятия незамкнутой и замкнутой ломаной линии (рис. 16). Учащиеся строят из палочек ломаную линию, находят ее начало (начало первого отрезка) и конец (конец последнего отрезка). Учитель дает название такой ломаной – незамкнутая, а затем предлагает по образцу соединить начало и конец незамкнутой ломаной линии. Учащиеся сами догадываются, что такая ломаная линии называется замкнутой. При этом звенья соединяют так, чтобы они, кроме вершин, не имели общих точек.

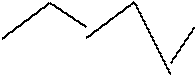Рис. 16

В процессе упражнений устанавливается связь между замкнутой ломаной линией и многоугольником, для которого ломаная линия является границей: замкнутая ломаная линия из трех звеньев ограничивает треугольник, из четырех звеньев – четырехугольник и т.д.

Затем учащихся знакомят с измерением ломаных линий таким способом: измерить звенья ломаной и сложить полученные числа. Чтобы дети усвоили понятие длины ломаной линии, необходимо включить достаточное количество упражнений в нахождении длины незамкнутых и замкнутых ломаных линий, которые содержат различное число звеньев.

Понятие о периметре многоугольника дается в процессе решения конкретной задачи на нахождение длины замкнутой ломаной линии. Учитель поясняет, что сумма длин всех сторон многоугольника называется его периметром. Можно на этом же уроке дать обозначение периметра буквой (Р = 24 см). сначала лучше включать задачи на нахождение периметра многоугольника с неравными сторонами, в процессе решения которых закрепляется понятие о длине ломаной линии. Затем специально рассматривается нахождение периметра равносторонних многоугольников, а также нахождение периметра прямоугольника. Периметр этих фигур дети сначала находят путем измерения их сторон и сложения полученных чисел. Но тут же обращается внимание на свойства этих фигур – равенство всех сторон или равенство противоположных сторон. Учащиеся делают вывод о возможности сократить измерения: при нахождении периметра равностороннего треугольника, квадрата и других многоугольников с равными сторонами достаточно измерить одну сторону, а затем умножить ее длину на число сторон многоугольника. При нахождении периметра прямоугольника достаточно узнать его длину и ширину (т.е. основание и высоту), затем умножить каждое из этих чисел на 2 и полученные произведения сложить. Опираясь на чертеж, они подмечают, что можно поступить по-другому: найти сумму длин смежных сторон, а затем умножить эту сумму на 2. Сравнивая полученные записи, например: Р = 4 ^. 2 + 6 ^. 2 и Р = (4 + 6) ^. 2, дети устанавливают, что во втором случае умножали сумму на число, а в первом – каждое слагаемое умножали на это число и результаты складывали. Так как использованное свойство умножения суммы на число известно детям, то они убеждаются в правильности своих рассуждений при нахождении периметра прямоугольника.

В дальнейшем во II и IV классах систематически решают задачи на вычисление периметра, а также задачи, им обратные. При решении которых полезно выполнять чертежи (хотя бы схематические). Наряду с решением готовых задач рекомендуется предлагать детям задания на составление подобных задач с геометрическим содержанием (подобрать и вставить в условие пропущенные числовые значения; составить задачу, обратную решенной; составить задачу по данной формуле вычисления периметра и т.п.). В процессе таких упражнений формируется понятие периметра многоугольника и умение находить его, а также развиваются пространственные и геометрические представления. [1, с.273, 274]

Заключение

Важнейшей задачей учителя является определение методики, раскрывающей содержание геометрического материала на том уровне, который должен быть достигнут учащимися к моменту перехода в V класс, а также ведущих направлений изучения этого материала.

Для формирования геометрических представлений работа должна проводиться следующим образом: свойства фигур учащиеся выделяют экспериментально, одновременно усваивают необходимую терминологию и навыки; основное место в обучении должны занимать практические работы учеников, наблюдения и работы с геометрическими объектами.

Геометрический материал не выделяется в программе и в реальном процессе обучения в качестве самостоятельного раздела. Вопросы геометрического содержания рассматриваются всегда, когда это оказывается возможным, в тесной связи с рассмотрением остальных вопросов курса.

Как правило, более высокого уровня усвоения достигают те учителя, которые, понимая самостоятельную значимость геометрических знаний, стремятся осуществить связь изучения геометрического материала с другим материалом начального курса математики. В основе этой связи лежит возможность установления отношений между числом и фигурой при формировании понятий числа, свойств числа, операций над ними и, наоборот, использовать числа для изучения свойств геометрических образов и их отношений.

В I классе фигуры следует применять наряду с другими материальными вещами как объекты для пересчитывания. Несколько позже такими объектами должны стать элементы фигур, например вершины, стороны, углы многоугольников.

Уже в I – IV классах выполняются простейшие классификации углов (прямые и непрямые), многоугольников (по числу углов) и т.д. Изучение родовых и видовых понятий готовит детей к пониманию определений, построенных на указании рода и видовых отличий.

Это дает, например, возможность построить методику ознакомления с прямоугольниками таким образом, что в дальнейшем ученики усваивают, что любой квадрат есть прямоугольник.

Использование упражнений, в которых дети отмечают (выделяют) точки, принадлежащие или не принадлежащие фигуре или нескольким фигурам, помогает в дальнейшем трактовать геометрическую фигуру как множество точек. А это позволяет более осознанно выполнять операции деления фигуры на части или получения фигуры из других (складывание), т.е. выполнять по существу операции объединения, пересечения, дополнения над точечными множествами.

Важной общей методической линией осуществления связи в изучении геометрического материала с остальными вопросами курса начальной математики является, таким образом, неявная опора на теоретико-множественные и простейшие логико-математические представления в изучении фигур, их отношений, свойств.

Работа по формированию навыков должна проводиться распределено и постепенно почти на каждом уроке (и не только на уроках математики). Это создает условия для более частого применения этих навыков в учебной и практической деятельности, обеспечивает необходимую их прочность.

Список использованной литературы

1. Бантова М.А., Бельтюкова Г.В. Методика преподавания математики в начальных классах. Пособие для пед. училищ. М., «Просвещение», 1984.

2. Истомина Н.Б. Методика преподавания математики в начальных классах. М., «Изд. центр «Академия», 1998.

3. Моро М.И., Пышкало А.М. Методика обучения математики в I – III классах. Пособие для учителя. Изд. 2-е перераб. и доп. М., «Просвещение»,1978.

Не нашли, что искали? Воспользуйтесь поиском: