
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Алгоритм Брезенхема для генерации окружности.
В растр нужно разлагать не только линейные, но и другие, более сложные функции. Разложению конических сечений, т. е. окружностей, эллипсов, парабол, гипербол, было посвящено значительное число работ. Наибольшее внимание, разумеется, уделено окружности. Один из наиболее эффективных и простых для понимания алгоритмов генерации окружности принадлежит Брезенхему. Для начала заметим, что необходимо сгенерировать только одну восьмую часть окружности. Остальные ее части могут быть получены последовательными отражениями, как это показано на рис. 5.1. Если сгенерирован первый октант (от 0 до 45° против часовой стрелки), то второй октант можно получить зеркальным отражением относительно прямой у = х, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой х = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = 0 для завершения построения. На рис. 5.1 приведены двумерные матрицы соответствующих преобразований.

|
Рис. 5.1. Генерация полной окружности из дуги в первом октанте.
Для вывода алгоритма рассмотрим первую четверть окружности с центром в начале координат. Заметим, что если работа алгоритма начинается в точке х = 0, у = R, то при генерации окружности по часовой стрелке в первом квадранте у является монотонно убывающей функцией аргументам (рис. 5.2). Аналогично, если исходной точкой является у = 0, х == R, то при генерации окружности против часовой стрелки х будет монотонно убывающей функцией аргумента у. В нашем случае выбирается генерация по часовой стрелке с началом в точке х = 0, у = R. Предполагается, что центр окружности и начальная точка находятся точно в точках растра.
Для любой заданной точки на окружности при генерации по часовой стрелке существует только три возможности выбрать следующий пиксел, наилучшим образом приближающий окружность: горизонтально вправо, по диагонали вниз и вправо, вертикально вниз. На рис. 5.3 эти направления обозначены соответственно mH, mD, mV. Алгоритм выбирает пиксел, для которого минимален квадрат расстояния между одним из этих пикселов и окружностью, т. е. минимум из
mH = |(xi + 1)2 + (yi)2 -R2|
mD = |(xi + 1)2 + (yi -1)2 -R2|
mV = |(xi)2 + (yi -1)2 -R2|
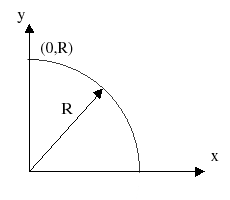 Рис. 5.2. Окружность в первом квадранте.
Рис. 5.2. Окружность в первом квадранте.
|  Рис.5.3. Выбор пикселов в первом квадранте.
Рис.5.3. Выбор пикселов в первом квадранте.
|
Вычисления можно упростить, если заметить, что в окрестности точки (xi,yi,) возможны только пять типов пересечений окружности и сетки растра, приведенных на рис. 5.4.

|
Рис. 5.4. Пересечение окружности и сетки растра.
Разность между квадратами расстояний от центра окружности до диагонального пиксела (xi, + 1, уi - 1) и от центра до точки на окружности R2 равна
i = (xi + 1)2 + (yi -1)2 -R2
Как и в алгоритме Брезенхема для отрезка, для выбора соответствующего пиксела желательно использовать только знак ошибки, а не ее величину.
При i < 0 диагональная точка (xi, + 1, уi - 1) находится внутри реальной окружности, т. е. это случаи 1 или 2 на рис. 5.4. Ясно, что в этой ситуации следует выбрать либо пиксел (xi, + 1, у i), т. е. mH, либо пиксел (xi, + 1, у i - 1), т. е. mD. Для этого сначала рассмотрим случай 1 и проверим разность квадратов расстояний от окружности до пикселов в горизонтальном и диагональном направлениях:
= |(xi + 1)2 + (yi)2 -R2| - |(xi + 1)2 + (yi -1)2 -R2|
При < 0 расстояние от окружности до диагонального пиксела больше, чем до горизонтального. Напротив, если > 0, расстояние до горизонтального пиксела больше. Таким образом,
при <= 0 выбираем mH в (xi, + 1, уi - 1)
при > 0 выбираем mD в (xi, + 1, уi - 1)
При = 0, когда расстояние от окружности до обоих пикселов одинаковы, выбираем горизонтальный шаг.
Количество вычислений, необходимых для оценки величины , можно сократить, если заметить, что в случае 1
(xi + 1)2 + (yi)2 -R2 >= 0
(xi + 1)2 + (yi -1)2 -R2 < 0
так как диагональный пиксел (xi, + 1, у i - 1) всегда лежит внутри окружности, а горизонтальный (xi, + 1, у i) - вне ее. Таким образом, можно вычислить по формуле
= (xi + 1)2 + (yi)2 -R2 + (xi + 1)2 + (yi -1)2 -R2
Дополнение до полного квадрата члена (yi)2 с помощью добавления и вычитания - 2yi + 1 дает
= 2[(xi + 1)2 + (yi -1)2 -R2] + 2yi - 1
В квадратных скобках стоит по определению i и его подстановка
= 2(i + yi) - 1
существенно упрощает выражение.
Рассмотрим случай 2 на рис. 5.4 и заметим, что здесь должен быть выбран горизонтальный пиксел (xi, + 1, уi), так как.у является монотонно убывающей функцией. Проверка компонент показывает, что
(xi + 1)2 + (yi)2 -R2 < 0
(xi + 1)2 + (yi -1)2 -R2 < 0
поскольку в случае 2 горизонтальный (xi, + 1, уi) и диагональный (xi, + 1, уi -1) пикселы лежат внутри окружности. Следовательно, < 0, и при использовании того же самого критерия, что и в случае 1, выбирается пиксел (xi, + 1, уi).
Если i > 0, то диагональная точка (xi, + 1, уi -1) находится вне окружности, т. е. это случаи 3 и 4 на рис. 5.4. В данной ситуации ясно, что должен быть выбран либо пиксел (xi, + 1, уi -1), либо (xi,, уi -1). Аналогично разбору предыдущего случая критерий выбора можно получить, рассматривая сначала случай 3 и проверяя разность между квадратами расстояний от окружности до диагонального mD и вертикального mV пикселов,
т. е. ' = |(xi + 1)2 + (yi -1)2 -R2| - |(xi)2 + (yi -1)2 -R2 |
При ' < 0 расстояние от окружности до вертикального пиксела (xi,, уi -1) больше и следует выбрать диагональный шаг к пикселу (xi, + 1, уi -1). Напротив, в случае '> 0 расстояние от окружности до диагонального пиксела больше и следует выбрать вертикальное движение к пикселу (xi,, уi -1). Таким образом,
при ' <= 0 выбираем mD в (xi +1,, уi -1)
при '> 0 выбираем mV в (xi,, уi -1)
Здесь в случае ' = 0, т. е. когда расстояния равны, выбран диагональный шаг.
Проверка компонент ' показывает, что
(xi)2 + (yi -1)2 -R2 >= 0
(xi + 1)2 + (yi -1)2 -R2 < 0
поскольку для случая 3 диагональный пиксел (xi +1, уi -1) находится вне окружности, тогда как вертикальный пиксел (xi,, уi -1) лежит внутри ее. Это позволяет записать ' в виде
' = (xi +1)2 + (yi -1)2 -R2 + (xi)2 + (yi -1)2 -R2
Дополнение до полного квадрата члена (xi)2 с помощью добавления и вычитания 2xi + 1 дает
' = 2[(xi +1)2 + (yi -1)2 -R2] - 2xi - 1
Использование определения i приводит выражение к виду
' = 2(i - xi )- 1
Теперь, рассматривая случай 4, снова заметим, что следует выбрать вертикальный пиксел (xi, уi -1), так как у является монотонно убывающей функцией при возрастании х.
Проверка компонент ' для случая 4 показывает, что
(xi +1)2 + (yi -1)2 -R2 > 0
(xi)2 + (yi -1)2 -R2 > 0
поскольку оба пиксела находятся вне окружности. Следовательно, ' > 0 и при использовании критерия, разработанного для случая 3, происходит верный выбор mV.
Осталось проверить только случай 5 на рис. 5.4, который встречается, когда диагональный пиксел (xi,, уi -1) лежит на окружности, т. е. i = 0. Проверка компонент показывает, что
(xi +1)2 + (yi)2 -R2 > 0
(xi +1)2 + (yi -1)2 -R2 = 0
Следовательно, > 0 и выбирается диагональный пиксел (xi +1, уi -1). Аналогичным образом оцениваем компоненты ':
(xi +1)2 + (yi -1)2 -R2 = 0
(xi +1)2 + (yi -1)2 -R2 < 0
и ' < 0, что является условием выбора правильного диагонального шага к (xi +1, уi -1). Таким образом, случай i = 0 подчиняется тому же критерию, что и случай i < 0 или i > 0. Подведем итог полученных результатов:
i < 0
<= 0выбираем пиксел (xi +1, уi) - mH
> 0 выбираем пиксел (xi +1, уi -1) - mD
i > 0
' <= 0 выбираем пиксел (xi +1, уi -1) - mD
' > 0 выбираем пиксел (xi, уi -1)- mV
i = 0 выбираем пиксел (xi +1, уi -1) - mD
Легко разработать простые рекуррентные соотношения для реализации пошагового алгоритма. Сначала рассмотрим горизонтальный шаг mH к пикселу (xi + 1, уi). Обозначим это новое положение пиксела как (i + 1). Тогда координаты нового пиксела и значение i равны
xi+1 = xi +1
yi+1 = yi
i+1 = (xi+1 +1)2 + (yi+1 -1)2 -R2 i + 2xi+1+ 1
Аналогично координаты нового пиксела и значение i для шага mD к пикселу (xi + 1, уi -1) таковы:
xi+1 = xi +1
yi+1 = yi -1
i+1 = i + 2xi+1 - 2yi+1 +2
То же самое для шага mV к (xi, уi -1)
xi+1 = xi
yi+1 = yi -1
i+1 = i - 2yi+1 +1
Реализация алгоритма Брезенхема на псевдокоде для окружности приводится ниже.
Пошаговый алгоритм Брезенхема для генерации окружности в первом квадранте
все переменные - целые
инициализация переменных
xi = 0
yi = R
i =2(1 - R)
Предел = 0
1 Plot (xi, yi
if yi <= Предел then 4
Выделение случая 1 или 2, 4 или 5, или 3
if i < 0 then 2
ifi > 0 then 3
if i= 0 then 20
определение случая 1 или 2
2 = 2i+ 2уi - 1
if <= 0 then 10
if > 0 then 20
определение случая 4 или 5
3 = 2i+ 2хi - 1
if <= 0 then 20
if > 0 then 30
выполнение шагов
шаг к mH
10 хi = хi + 1
i = i+ 2хi + 1
Gо to 1
шагmD
20 хi = хi + 1
yi = yi + 1
i = i+ 2хi - 2уi+ 2
Gо to 1
Finish
Переменная предела устанавливается в нуль для окончания работы алгоритма на горизонтальной оси, в результате генерируется окружность в первом квадранте. Если необходим лишь один из октантов, то второй октант можно получить с помощью установки Предел = Integer (R/sqrt(2)), а первый - с помощью отражения второго октанта относительно прямой у = х (рис. 5.1). Блок-схема алгоритма приводится на рис. 5.5.

|
Рис. 5.5. Блок-схема пошагового алгоритма Брезенхема для генерации окружности в первом квадранте.
Пример 5.1. Алгоритм Брезенхема для окружностию
Рассмотрим окружность радиусом 8 с центром в начале координат. Генерируется только первый квадраннт.
начальные установки
x = 0
y = 8
= 2(1-8) = -14
Предел = 0
Пошаговое выполнение основного цикла
1 Plot (0,8)
yi > Предел (продолжать)
i < 0 go to 2
2 go to 10
10 x = 0+1 = 1
i = -14 +2 + 1 = -11
go to 1
1 Plot (1,8)
yi > Предел (продолжать)
i < 0 go to 2
2 go to 10
10 x = 1+1 = 1
i = -11 +2(2) + 1 = -6
go to 1
1 Plot (2,8)
...
Продолжать
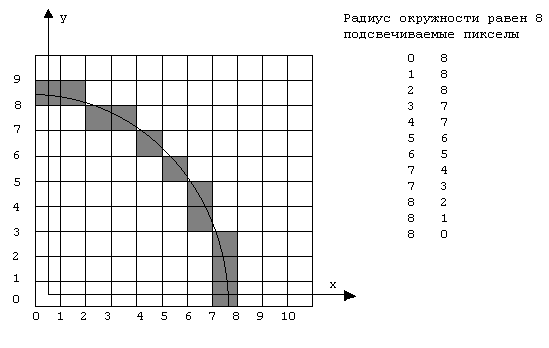
Результаты всех последовательных проходов алгоритма сведены в таблицу. Список пикселов выбранных алгоритмов состоит из (0,8), (1,8), (2,8), (3,7), (4,7), (5,6), (6,5), (7,4), (7,3), (8,2), (8,1), (8,0).
| Plot | i | | ' | x | y |
| -14 | |||||
| (0,8) | |||||
| -11 | -13 | ||||
| (1,8) | |||||
| -6 | -7 | ||||
| (2,8) | |||||
| -12 | |||||
| (3,7) | |||||
| -3 | |||||
| (4,7) | |||||
| -3 | |||||
| (5,6) | |||||
| (6,5) | |||||
| -11 | |||||
| (7,4) | |||||
| (7,3) | |||||
| -7 | |||||
| (8,2) | |||||
| (8,1) | |||||
| (8,0) |
алгоритм завершен.
Результаты показаны на рис.5.6. вместе с реальной окружностью. Алгоритм легко обобщается для других квадрантов или дуг окружностей.
|
Рис. 5.6. Результаты работы пошагового алгоритма Брезенхема генерации окружности.
Не нашли, что искали? Воспользуйтесь поиском: