Алгоритм принятия решения

Нечеткие логические уравнения (8.4)-(8.6) вместе с функциями принадлежности нечетких термов (8.7) позволяют принимать решение об уровне ИБС по следующему алгоритму:

1°. Зафиксируем значения параметров состояния больного

.

2°. Используя модель (8.7) и параметры 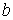и из табл. 8.4, определим значения функций принадлежности , при фиксированных значениях параметров , .

3°. Используя логические уравнения (8.4)-(8.6), вычислим значения функций принадлежности при векторе состояния для всех диагнозов . При этом, логические операции И() и ИЛИ(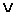) над функциями принадлежности заменяются операциями и :

,

.

4°. Определим решение , для которого:

.

Пример 8.1. Пусть некоторому больному соответствуют следующие количественные значения параметров состояния:

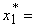53 лет, 175 у.е., 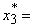507 кгм/мин,

2.4 у.е., 0.25 у.е., 60.7 ммоль/л,

26.14 ммоль/л, 10.4 ммоль/л, 3.9 у.е.,

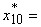22.4 млитр/мин кг, 172 у.е., 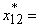26.1 у.е.

Используя модель (8.7) и значения параметров 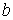и из табл. 8.4 находим значения функций принадлежности в точках , для всех нечетких термов и представим их в табл. 8.5.

Подставляя полученные значения в уравнение (8.5), находим:

Аналогично: , , , .

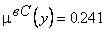В соответствии с уравнением (8.6):

Аналогично: , , , .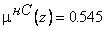

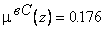Таблица 8.5.

Значения функций принадлежности

№
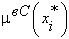
		3.259	0.074	0.143	0.349	0.927	0.608
		0.679	0.649	0.892	0.328	0.136	0.072
		1.503	0.274	0.771	0.775	0.275	0.120
	2.4	2.182	0.152	0.379	0.963	0.560	0.205
	0.25	1.362	0.315	0.867	0.676	0.241	0.109
	60.7	2.996	0.087	0.176	0.462	1.000	0.458
	26.14	3.255	0.074	0.142	0.343	0.911	0.635
	10.4	1.157	0.389	0.972	0.545	0.201	0.095
	3.9	2.468	0.123	0.283	0.795	0.751	0.266
	22.4	1.791	0.210	0.576	0.951	0.368	0.149
		1.647	0.239	0.670	0.872	0.318	0.133
	26.1	3.376	0.070	0.131	0.310	0.857	0.687

Наконец, в соответствии с уравнением (8.4) находим:

Аналогично: , , , , .

Поскольку наибольшее значение функции принадлежности соответствует решению , то в качестве диагноза выбираем НЦД тяжелой степени.

Не нашли, что искали? Воспользуйтесь поиском: