Ряд Тейлора и Маклорена

Лекции 33,34. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд (4ч)

Содержание лекции:

Ряды Тейлора и Маклорена. Разложение функции в степенной ряд, необходимое, достаточные условия. Приложения степенных рядов. Примеры.

Разложение в ряд Маклорена некоторых элементарных функций. Приближенное вычисление значений функции с помощью степенных рядов.

Ряд Тейлора и Маклорена

Пусть дана функция f (x), непрерывная на некотором множестве D и х ₀Î D. Если $ сходящийся степенной ряд 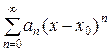такой, что сумма этого ряда совпадает с f (x) в некоторой окрестности точки х ₀,, т.е.

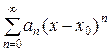= f (x),

то говорят, что функция f (x) разлагается в степенной ряд в окрестности точке х ₀ (или в ряд по степеням х – х ₀).

Теорема 2.

Если функция f (x) разлагается в ряд по степеням (х – х ₀), то коэффициенты этого ряда равны .

Доказательство. Пусть в окрестности х ₀ справедливо разложение

f (x) = а ₀ + а ₁(х – х ₀) + а ₂(х – х ₀)² + а ₃(х – х ₀)³ + а ₄(х – х ₀)⁴ +... (3)

Положим в этом равенстве х = х ₀, получим а ₀ = f (x ₀).

Так как ряд в окрестности х ₀ сходится, то его можно дифференцировать. Продифференцируем равенство (3) п раз, получим

f¢ (x) = а ₁ +2 а ₂(х – х ₀) + 3 а ₃(х – х ₀)² + 4 а ₄(х – х ₀)³ +...,

f¢¢ (x) = 2 а ₂+ 6 а ₃(х – х ₀) +12 а ₄(х – х ₀)² +...,

f¢¢¢ (x) = 6 а ₃+ 24 а ₄(х – х ₀) +...,

..........................

f ^(п) (x) = п (п –1)(п –2)...2 а_п + (п +1) п (п– 1)...2 а_{п +1}(х – х ₀) +...

Полагая в этих равенствах х = х ₀, получим

f¢ (x ₀) = а ₁, или а ₁= f¢ (x ₀),

f¢¢ (x ₀) = 2 а ₂, откуда ,

f¢¢¢ (x ₀) = 6 а ₃, откуда ,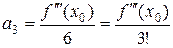

.............

f ^(п) (x ₀) = п (п –1)(п –2)...2 а_п, откуда 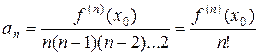. ЧТД.

Определение 1. Степенной ряд 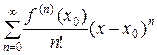называется рядом Тейлора в точке х ₀ для функции f (x), а коэффициенты этого ряда называются коэффициентами Тейлора для функции f (x).

Из теоремы 7.2. следует:

1) если функция f (x) разлагается в степенной ряд в окрестности точки х ₀, то это есть обязательно ряд Тейлора этой функции:

f (x) = .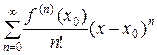

2) Если функция f (x) разложима в степенной ряд в окрестности точки х ₀, то она бесконечное число раз дифференцируема в этой окрестности (это свойство называют необходимым условием разложимости в степенной ряд).

Теорема 7.2. формулирует необходимое, но не достаточное условие разложимости функции в степенной ряд. Т.е. нельзя утверждать, что ряд Тейлора, формально составленный для функции f (x), сходится обязательно к этой функции.

Например, функция бесконечно дифференцируема в окрестности нуля, но ее ряд Тейлора имеет совершенно другую сумму.

Достаточные условия сходимости ряда Тейлора к самой функции (т.е. разложимости функции в степенной ряд) дает следующая

Теорема 3.

Для того чтобы функция f (x) могла быть разложена в степенной ряд (ряд Тейлора) в окрестности U(x ₀) точки х ₀, необходимо и достаточно, чтобы остаток этого ряда стремился к нулю при п ®¥ " х из этой окрестности, т.е.

f (x) = 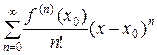Û

для всех х ÎU(x ₀).

При этом исследование поведения остатка ряда удобно проводить, используя различные формы записи остатка ряда, в частности форму Лагранжа:

,

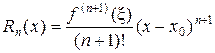где x – некоторое число, удовлетворяющее условию 0 < |x – x ₀| < | x – x ₀|, т.е. число x расположено между х и х ₀.

Определение 2.

Функция, которая на некотором интервале может быть представлена своим сходящимся рядом Тейлора, называется аналитической на этом интервале.

Из определения следует, что сумма сходящегося степенного ряда есть аналитическая функция в интервале сходимости ряда.

Не нашли, что искали? Воспользуйтесь поиском: