
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приложения степенных рядов
Рассмотрим примеры применения степенных рядов к решению различных задач.
Пример 5. Вычислить число е с точностью 0,001.
Используем разложение ех =  , х Î R, положим здесь х = 1. Получим
, х Î R, положим здесь х = 1. Получим
е =  . Так как S – S n = R n, то чтобы найти частичную сумму S n так, чтобы она отличалась от истинной суммы не более чем на 0,001, нужно, чтобы соответствующий остаток ряда так же был не больше 0,001. Оценим остаток ряда, используя форму Лагранжа:
. Так как S – S n = R n, то чтобы найти частичную сумму S n так, чтобы она отличалась от истинной суммы не более чем на 0,001, нужно, чтобы соответствующий остаток ряда так же был не больше 0,001. Оценим остаток ряда, используя форму Лагранжа:
 , откуда имеем
, откуда имеем  .
.
Учитывая оценки  , получим (п +1)! ³ 3000.
, получим (п +1)! ³ 3000.
Находим:
| п = 1 2! = 2; п =2 3! = 6; п = 3 4! =24; | п = 4 5!= 120; п = 5 6! = 720; п = 6 7! = 4320 > 3000 |
Таким образом, при п = 6 остаток ряда будет меньше 0,001. Значит, чтобы найти значение е с точностью 0,001, нужно в заданном ряде отбросить все члены, начиная с члена с номером 7, оставшаяся сумма даст искомое приближение:
е» 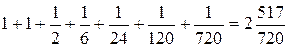 =2,718
=2,718
Пример 6. Вычислить  с точностью до 0,001. Заданный интеграл можно найти непосредственно по формуле Ньютона-Лейбница, при этом придется 4 раза применить интегрирование по частям. Мы же разложим в ряд по степеням х подынтегральную функцию и проинтегрируем получившийся ряд:
с точностью до 0,001. Заданный интеграл можно найти непосредственно по формуле Ньютона-Лейбница, при этом придется 4 раза применить интегрирование по частям. Мы же разложим в ряд по степеням х подынтегральную функцию и проинтегрируем получившийся ряд:

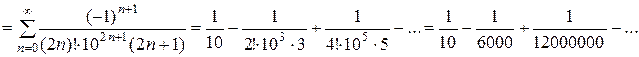
Получили знакочередующийся ряд, удовлетворяющий теореме Лейбница. Значит, для оценки остатка R n этого ряда достаточно найти слагаемое, меньшее 0,001, и начиная с него, отбросить все последующие члены ряда. Оставшееся даст искомый результат. Таким членом является второй, значит  » 0,1 с точностью до 0,001.
» 0,1 с точностью до 0,001.
Степенные ряды широко применяются при решении дифференциальных уравнений.
Пример 7. Найти 4 первых члена разложения решения дифференциального уравнения  ,
, 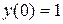 .
.
Пусть  – искомое решение заданного дифференциального уравнения. Так как эта функция непрерывная, то она представима в виде ряда Тейлора:
– искомое решение заданного дифференциального уравнения. Так как эта функция непрерывная, то она представима в виде ряда Тейлора:
 .
.
По условию задачи, требуется найти решение, удовлетворяющее начальному условию 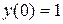 , т.е. в окрестности точки
, т.е. в окрестности точки 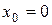 . Следовательно, записанный выше ряд является рядом Маклорена:
. Следовательно, записанный выше ряд является рядом Маклорена:
 .
.
Используя заданное уравнение и начальное условие, найдем четыре первых коэффициента этого степенного ряда.
Имеем 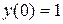 .
.
Запишем заданное уравнение в виде  . Подставив сюда
. Подставив сюда 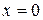 , получим
, получим
 , откуда
, откуда  .
.
Далее, дифференцируя уравнение  , получим
, получим
 ,
,
 ,
,
откуда, при 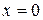 имеем
имеем
 ,
,
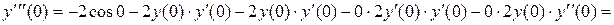
 .
.
Подставляя найденные коэффициенты в ряд Маклорена, получим
 .
.
Пример 8. Найти три первых отличных от нуля члена разложения в степенной ряд решения дифференциального уравнения  ,
,  .
.
Так как  , то решение ищем в виде
, то решение ищем в виде
 .
.
Имеем: 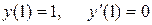 . Из заданного уравнения находим
. Из заданного уравнения находим
 .
.
Дифференцируя уравнение, получим
 ,
,  .
.
Тогда искомое разложение решения в ряд имеет вид:
 .
.
Не нашли, что искали? Воспользуйтесь поиском: