Коэффициент асимметрии Пирсона

х - Мо

As = -------

s

Оценка степени существенности этого показателя дается с помощью средней квадратической ошибки, рассчитываемой по формуле

6 (n – 1)

s As = ----------

Ö (n+1) (n +3)

где n – число наблюдений.

Если çAs ç / s As > 3, асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если же çAs ç / s As < 3,, асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.

Для симметричных распределений рассчитывается показатель эксцесса (островершинности):

m₄

Е _х = ----- - 3

s⁴

где m₄ - центральный момент четвертого порядка.

Средняя квадратическая ошибка эксцесса исчисляется по формуле

24n (n – 2) (n – 3)

s Е _х = -------------------------

Ö (n – 1) ² (n + 3) (n + 5)

где n – число наблюдений.

Для приближенного определения величины эксцесса может быть использована формула Линдберга:

Е_х = П – 38,29

где П – процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения в ту и другую сторону от величины средней, в общем количестве вариант данного ряда; 38,29 – процент количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения, в общем количестве вариант ряда нормального распределения..

Кривая Пауссона, выражение которой

а^х\е^-а

Р_х = -------

хi

где Р_х – вероятность наступления отдельных значений х

а = х – средняя арифметическая ряда.

Теоретические частоты при выравнивании эмпирических данных по кривой Пуассона определяются по формуле

¦’ = NP_x

где ¦’ – теоретические частоты; N – общее число единиц ряда.

Для оценки близости эмпирических (¦) и теоретических (¦’) частот можно применить один из критериев согласия6 критерий Пирсона (c² - «хи-квадрат»), критерий Романовского, критерий Колмогорова (l - «лямбда»).

Критерий Пирсона (c²) представляет собой сумму отношений квадратов расхождений между ¦ и ¦’ к теоретическим частотам:

(¦ - ¦’)²

c² = S -----------

¦’

Полученное значение критерия (c² расч) сравнивается с табличным значением (c²табл). Последнее определяется по специальной таблице в зависимости от принятой вероятности (Р) и числа степеней свободы (n - «ню»)

Уровень значимости (a) – вероятность допуска ошибки первого рода, т.е. вероятность отвергнуть правильную гипотезу о законе распределения, - обычно принимается равным 5 или 1% (a = 0,05 или a = 0,01).

Число степеней свободы (n) рассчитывается как число групп (m) в ряду распределения минус число параметров эмпирического распределения, использованных для нахождения теоретических частот.

Если выравнивание осуществляется не по частотам (¦), а по частостям

¦_i (w_{i -} w_i’)²

w_{i = --------} то c² рассчитывается по формуле c² = N S ------------

S ¦_i w_i’

где w_i, w_i’ – частости соответственно эмпирического и теоретического распределения, N = S ¦_i- общая сумма частот (абсолютная численность единиц распределения).

При отсутствии таблиц значений c² для оценки случайности расхождений теоретических и эмпирических частот можно воспользоваться критерием Романовского

çc² - n ç

--------

Ö 2n

Если указанное отношение меньше 3, то расхождение считаются случайными, если больше 3, то они существенны.

Критерий Колмогорова (l) основан на определении максимального расхождения между накопленными частостями эмпирического и теоретического распределений:

l = d ÖN

где d – максимальная величина расхождений между накопленными частостями;

N - число наблюдений, или сумма всех частот.

Если пользоваться не накопленными частостями, а частотами (абсолютными показателями), то формула примет вид

D

l= ---------

Ö N

где D - максимальная разность между накопленными частотами;

N - сумма всех частот.

При проведении выборочного наблюдения используются следующие показатели:

N – объем генеральной совокупности (число входящих в нее единиц)

n – объем выборочной совокупности (число единиц, попавших в выборку)

x – генеральная средняя (среднее значение признака в генеральной совокупности)

x – выборочная средняя (среднее значение признака в выборочной совокупности)

p – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)

w – выборочная доля (доля единиц, обладающих данным признаком в выборочной совокупности)

s² - генеральная дисперсия (дисперсия признака в генеральной совокупности)

S² – выборочная дисперсия (дисперсия признака в выборочной совокупности)

s - среднее квадратическое отклонение признака в генеральной совокупности

S - среднее квадратическое отклонение признака в выборочной совокупности.

При бесповторном способе отбора формула для расчета стандартной ошибки будет:

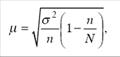
где 1 – n / N – доля единиц генеральной совокупности, не попавших в выборку.

При определении стандартных ошибок типической выборки применяются следующие формулы:

• при повторном способе отбора

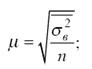
• при бесповторном способе отбора:

– средняя из групповых дисперсий в выборочной совокупности.

В формуле предельной ошибки выборки учитывается средняя из групповых дисперсий (s²), т.е.

s² w( 1- w) t² s²

D = tm = t ---- или D = t --------- n = ----------

Ö n Ö n D²

Стандартная ошибка серийной в ыборки определяется по формулам:

• при повторном способе отбора –

где d– межсерийная дисперсия выборочной совокупности; r – число отобранных серий;

• при бесповторном способе отбора –

где R – число серий в генеральной совокупности.

Величина межсерийной д исперсии

S(x_i – x)²

d² = -----------------

s

s -число обследованных серий

Серийная выборка в основном проводится как бесповторная, и формула ошибки выборки в этом случае имеет вид

d² s

Δ = t --- 1 - ----

Ö s S

где d² - межсерийная дисперсия,

s - число отобранных серий,

S - число серий в генеральной совокупности.

При комбинированной выборке в сочетании использовались механическая и типическая выборки, то стандартную ошибку можно определить по формуле

где m1 и m2 – стандартные ошибки соответственно механической и типической выборок.

Стандартную ошибку выборки при многоступенчатом отборе при группах разных объемов определяют по формуле

где m1, m2, m3,... – стандартные ошибки на разных ступенях;

n1, n2, n3,... – численность выборок на соответствующих ступенях отбора.

Дисперсия возможных значений выборочной средней

s²r

μ²=-------

n

Исходя из этого средняя ошибка выборочной средней при повторном отборе определяется по формуле

s²r s

μ²= ------- = ------

Ö n Ö n

где s² - дисперсия изучаемого показателя в генеральной совокупности (так как дисперсия изучаемого показателя в генеральной совокупности неизвестна, то фактически в формулу подставляется выборочная дисперсия, которая при большом числе наблюдений близка к генеральной);

n - объем (численность) выборки.

Средняя ошибка выборки (μ) при повторном отборе зависит от показателя вариации (s) и от объема выборки (n).

Средняя ошибка выборочной доли определяется по формуле

w (1- w)

μ = __________

n

где w - выборочная доля единиц, обладающих изучаемым признаком, w (1- w) - дисперсия доли (альтернативного признака).

При бесповторном отборе в формах под знаком радикала появляется множитель

n

1 - ----

N

где N - численность генеральной совокупности.

Предельная ошибка выборки, обозначаемая через Δ, рассчитывается как t- кратная средняя ошибка, т.е.

Δ = t μ,

где μ - средняя ошибка выборки,

t - коэффициент доверия, т.е. показатель, зависящий от вероятности (Р), с которой предельная ошибка определяется.

Общая формула предельной ошибки выборки Δ = t μ для средней приобретает вид

s²

Δ = t --- (для повторного отбора),

Ö n

s² n

Δ = t --- 1 - ---- (для бесповторного отбора),

Ö n N

а для доли – соответственно

w (1 – w) w (1 – w) n

Δ = t ----------- и Δ = t ----------- 1 - ----

Ö n Ö n N

Теорема Чебышева

Р (çх – х ç < x) ® 1 при n ®¥

Теорема Бернулли является частным случаем теоремы Чебышева и касается расхождения между долями единиц, обладающих изучающим признаком, в выборочной и генеральной совокупности, т.е. разности ç w – p ç.

Согласно так называемой центральной предельной теореме Ляпунова, вероятность заданной предельной ошибки (Δ) может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:

t²

1 +t - ---

F(t) = P (ç x- x ç £ tm) = --- ò e ² dt

Ö 2p -t

где x- x

t = ------ - нормированное отклонение выборочной средней от

μ генеральной.

Значения интеграла Лапласа (Р) для разных t рассчитаны и приведены в специальных таблицах (приложение).

Так при t=1 вероятность Р = 0,683.

Это означает, что с вероятностью 0,683 (или 68,3%) можно гарантировать, что отклонение генеральной средней от выборочной не превысит однократной средней ошибки, т.е. что в генеральной совокупности среднее значение признака (х) будет находиться в пределах х – μ £ х £ х + μ

Индекс изменение товарооборота (агрегатный индекс товарооборота)

Количество - q, цена - p

Индивидуальный индекс цен определяется как отношение цены отдельного товара в отчтном периоде к цене его в базисном периоде i_p = p_i / p₀

Индекс Фишера:

Агрегатный индекс физического объема товарооборота

Агрегатный индекс себестоимости:

числитель представляет собой сумму фактических затрат на продукцию в отчетном периоде, а знаменатель – условную величину, которая показывает, сколько средств было бы затрачено на продукцию отчетного периода, если бы себестоимость единицы каждого вида продукции сохранялась на базисном уровне.

Сводный индекс цен

Расчет сводного индекса расхода материалов

Для индивидуальных объемных показателей (объем реализации, объем производительности продукции, посевная площадь) веса выбираются на уровне базисного периода. Например:

где In– сводный индекс урожайности; I – сводный индекс стоимости товарооборота; Iq – сводный индекс себестоимости.

Для индексов динамики с постоянными весами имеет силу взаимосвязь между цепными и базисными темпами роста (индексами):

Индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:

(агрегатная форма индекса Ласпейреса).

Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (г^) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:

Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq, тогда:

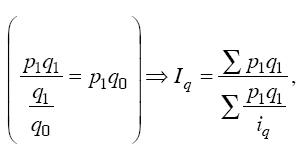
таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.

Не нашли, что искали? Воспользуйтесь поиском: