ОБРАЗЕЦ РЕШЕНИЯ ЗАДАНИЯ

ЗАДАНИЕ 1. Даны координаты вершин пирамиды : 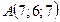, , , 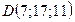. Выполнить следующие задания:

1. Написать уравнения основания и боковой грани пирамиды.

2. Доказать, что боковая грань перпендикулярна плоскости основания .

3. Написать уравнение плоскости, проходящей параллельно плоскости основания через середину ребра .

4. Написать уравнения ребер и , найти угол между ними.

5. Найти угол между ребром и плоскостью основания .

Решение.

1. Написать уравнения основания и боковой грани пирамиды.

а) Плоскость основания задана в пространстве координатами трех точек, лежащих в этой плоскости. Поэтому для написания уравнения плоскости используем уравнение (1.3):

.

Подставим в данное уравнение в качестве координат первой, второй, третьей точек координаты точек 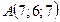, , соответственно, получим

или

.

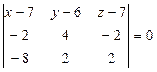Упростим правую часть уравнения, разложив определитель по первой строке:

,

.

Разделим обе части уравнения на 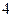, раскроем скобки и приведем подобные:

,

.

Таким образом, общее уравнение плоскости имеет вид .

б) Аналогично найдем уравнение плоскости , подставив в уравнение (1.3) координаты точек 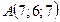, , 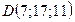. Получим:

,

.

,

,

,

.

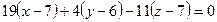
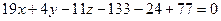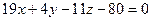Таким образом, общее уравнение плоскости имеет вид .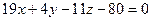

2. Доказать, что боковая грань перпендикулярна плоскости основания .

Чтобы доказать, что боковая грань перпендикулярна основанию , используем условие перпендикулярности двух плоскостей (1.6). Для этого нам нужны общие уравнения плоскостей и нормальные векторы к данным плоскостям.

Из общих уравнений плоскостей и , полученных в предыдущем пункте, найдем координаты нормальных векторов.

Напомним, что если общее уравнение плоскости имеет вид , то нормальный вектор имеет координаты .

В нашем случае имеем:

, где .

, где .

Из условия перпендикулярности плоскостей следует, что если скалярное произведение нормальных векторов рано нулю, то плоскости перпендикулярны.

Проверим данное условие для плоскостей и . Найдем скалярное произведение нормальных векторов и :

.

Т.к. скалярное произведение нормальных векторов равно нулю (векторы перпендикулярны), то плоскости и перпендикулярны.

Следовательно, боковая грань перпендикулярна основанию , что и требовалось доказать.

3. Написать уравнение плоскости, проходящей параллельно плоскости основания через середину ребра .

Искомая плоскость определена двумя условиями: проходит через середину ребра и параллельна плоскости .

Найдем координаты середины ребра . Пусть — искомая точка, тогда для нахождения её координат используем формулы для нахождения середины отрезка (4.1).

, , .

, , .

Таким образом, точка имеет координаты .

Из условия параллельности плоскостей (2.6) следует, что нормальные векторы параллельных плоскостей коллинеарны. В частности, нормальный вектор для одной из плоскостей является нормальным и для второй плоскости.

Таким образом, из условия следует, что нормальный вектор является нормальным и для плоскости , т.е. .

Итак, имеем, что искомая плоскость проходит через точку и вектор перпендикулярен ей. Тогда для написания уравнения плоскости будем использовать уравнение (1.1).

,

где 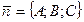— нормальный вектор, а — точка, лежащая в плоскости.

Для плоскости имеем:

,

,

,

.

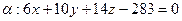Таким образом, общее уравнение плоскости имеет вид .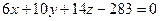

4. Написать уравнения ребер и , найти угол между ними.

а) Составим уравнения прямых и . Для этого используем уравнения прямой, проходящей через две заданные точки (2.4).

,

где — , координаты точек, принадлежащих данной прямой.

Подставим координаты точек , 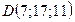в канонические уравнения прямой, получим уравнения прямой :

,

,

где 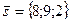направляющий вектор прямой .

Аналогично получим уравнения прямой , где , .

,

,

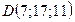где направляющий вектор прямой .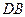

Таким образом, получили уравнения прямых:

, ,

, .

б) Пусть — искомый угол между ребрами и . Для нахождения угла между прямыми и подставим координаты направляющих векторов и в формулу (2.5).

,

где , .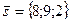

.

(значение угла можно вычислить по таблицам Брадиса или на калькуляторе).

5. Найти угол между ребром и плоскостью основания .

Для нахождения угла между прямой и плоскостью используем формулу (3.1).

,

где 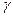— угол между плоскостью основания и ребром , 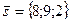— направляющий вектор прямой , — нормальный вектор плоскости .

Для угла 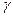имеем:

.

.

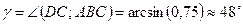Не нашли, что искали? Воспользуйтесь поиском: