Прямоугольная изометрическая проекция

Прямоугольная изометрическая проекция – одна из самых удобных проекций – аксонометрические оси х, у и z образуют друг с другом углы в 120°, а коэффициенты искажения по всем трем осям одинаковы и равны 0,82. В целях упрощения изометрическую проекцию выполняют, как правило, без искажения по осям, используя так называемый приведенный коэффициент искажения, равный 1. Каждый отрезок, направленный по осям x, y, z или параллельно им, сохраняет свою величину. Получаемое при этом изображение предмета в изометрической проекции имеет несколько большие размеры (в 1,22 раз), чем в действительности.

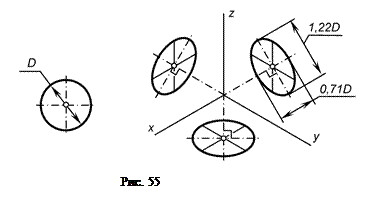
Изометрическими проекциями окружностей, расположенных в плоскостях, параллельных плоскостям проекций, являются эллипсы с одинаковыми соотношениями осей (рис. 55). Большие оси эллипсов перпендикулярны аксонометрической оси, отсутствующей в данной плоскости (например, если строится эллипс в горизонтальной плоскости проекций, его большая ось перпендикулярна оси z и т. п.).

Если изометрическую проекцию выполняют без искажения по осям х, у и z, то большие оси эллипсов равны 1,22 диаметра окружности, а малые — 0,71 диаметра. Если изометрическую проекцию выполняют с искажением, то большие оси эллипсов равны диаметру окружности, а малые оси — 0,58 диаметра окружности.

Линии штриховки наносят параллельно одной из диагоналей квадратов, лежащих в соответствующих плоскостях проекций, стороны которых параллельны аксонометрическим осям (рис. 56). Ребра жесткости, спицы маховиков и подобные элементы, попадающие в секущую плоскость, штрихуются.

Не нашли, что искали? Воспользуйтесь поиском: