
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
видовження тіла при деформації пропорційне величині деформуючої сили.
Слід сказати, що формула (16) – це теж по суті закон Гука, але написаний через інші фізичні величини.
Дослідженнями доведено, що закон Гука (абсолютна деформація пропорційна величині сили) є справедливим не лише для розтягнення-стискання, але й для інших видів деформацій у межах, поки їх можна вважати пружними.
Для визначення границь застосування закону Гука до певної речовини необхідно для тіла, виготовленого з цієї речовини, виконати експериментальні вимірювання для побудови діаграми напружень (залежності відносної деформації e від механічного напруження s). Приклад діаграми напружень наведено на рис. 3. Вона містить кілька характерних ділянок, границі яких визначають основні механічні параметри даної речовини.
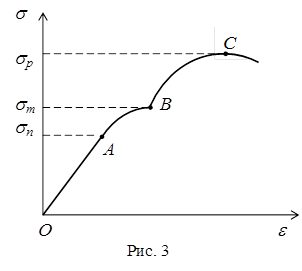 На ділянці ОА деформація змінюється у відповідності до закону Гука, тобто пропорційно до напруження. Найбільше механічне напруження sп, що відповідає цій ділянці, визначає границю пружності даної речовини. При подальшому зростанні механічного напруження його залежність від деформації є нелінійною, тобто закон Гука на цій ділянці (ділянка АВ) не виконується. В речовині при цьому виникають необоротні пластичні деформації. При наближенні до точки В деформація зростає практично без зростання механічного напруження (явище текучості речовини). Механічне напруження sт що відповідає верхній границі цієї ділянки діаграми, називається границею текучості речовини. При s > sт (ділянка ВС) відбувається руйнування тіла (розривання міжатомних зв’язків). Максимальне механічне напруження sр, що може бути досягнуте в тілі перед його остаточним руйнуванням, називається границею міцності речовини.
На ділянці ОА деформація змінюється у відповідності до закону Гука, тобто пропорційно до напруження. Найбільше механічне напруження sп, що відповідає цій ділянці, визначає границю пружності даної речовини. При подальшому зростанні механічного напруження його залежність від деформації є нелінійною, тобто закон Гука на цій ділянці (ділянка АВ) не виконується. В речовині при цьому виникають необоротні пластичні деформації. При наближенні до точки В деформація зростає практично без зростання механічного напруження (явище текучості речовини). Механічне напруження sт що відповідає верхній границі цієї ділянки діаграми, називається границею текучості речовини. При s > sт (ділянка ВС) відбувається руйнування тіла (розривання міжатомних зв’язків). Максимальне механічне напруження sр, що може бути досягнуте в тілі перед його остаточним руйнуванням, називається границею міцності речовини.
В) Сила тертя
Однією з найбільш широко розповсюджених є сила тертя. З досвіду відомо, що у більшості випадків тіло, приведене у стан руху з певною швидкістю, через деякий час зупиняється, якщо його рух не підтримується дією сил. Це стосується руху тіла у певному середовищі (рідкому або газоподібному) або руху відносно поверхні якогось іншого твердого тіла при наявності механічного контакту з цією поверхнею. У даному розділі ми розглянемо саме цей останній випадок.
Причиною тертя при ковзанні однієї поверхні по іншій є мікронерівності поверхонь, що дотикаються. Для дуже гладких поверхонь певну роль відіграють також сили міжмолекулярної взаємодії.
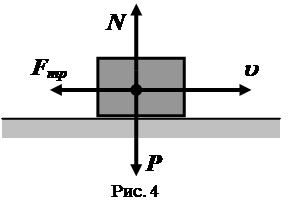 Під час руху тіла сила тертя
Під час руху тіла сила тертя  завжди має напрямок, протилежний напрямку вектора швидкості
завжди має напрямок, протилежний напрямку вектора швидкості 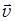 (Рис. 4).
(Рис. 4).
Модуль сили тертя пропорційний силі нормального тиску, з якою тіло тисне на поверхню. Згідно з ІІІ законом Ньютона, ця сила нормального тиску дорівнює по модулю силі реакції опори  , з якою поверхня тисне на тіло. Звідси:
, з якою поверхня тисне на тіло. Звідси:
 , ,
| (18) |
де k – коефіцієнт тертя, який залежить від складу та стану речовини, стану поверхні та деяких інших чинників.
Якщо тіло знаходиться на похилій площині (рис. 5), то на нього діють ті ж самі сили (вага тіла, реакція опори і сила тертя), але під певними кутами, які залежать від кута нахилу похилої площини a.
 Ковзання тіла вниз вздовж похилої площини буде відбуватися лише в тому випадку, коли векторна сума сили тяжіння і реакції опори перевищить по модулю силу тертя:
Ковзання тіла вниз вздовж похилої площини буде відбуватися лише в тому випадку, коли векторна сума сили тяжіння і реакції опори перевищить по модулю силу тертя:
F ³ Fтр.
Оскільки
| F = P sin a, | (19) |
| Fтр= k N = k P cos a, | (20) |
то в граничному випадку (коли F = Fтр):
P sin a0 = k P cos a0,
звідки:
| k = tg a0, | (15) |
тобто коефіцієнт тертя дорівнює тангенсу кута a0, при якому починається ковзання тіла по похилій площині.
ЗАВДАННЯ НА САМОПІДГОТОВКУ:
1. Опрацювати конспект лекції 1/3.
2. Повторити методику розв’язування задач, виконаних під час лекцій.
3. Виноградов А.Г. Курс фізики (частина І). § 1.3.
Вивчити теоретичний матеріал.
Дати відповіді на контрольні запитання.
Не нашли, что искали? Воспользуйтесь поиском: