ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Імпульс замкненої механічної системи зберігається(не змінюється з часом), які б процеси не відбувалися всередині системи.
Це один із фундаментальних законів природи, який виконується за будь-яких умов і не лише у рамках класичної механіки, але й у сучасній фізиці. Він стверджує, що тіла, які входять до складу замкненої механічної системи, можуть як завгодно взаємодіяти між собою, співударятися, змінювати свої імпульси, але загальний імпульс усієї замкненої системи при цьому не змінюється.
У ряді випадків для аналізу руху механічної системи корисно ввести поняття центру мас цієї системи. Положення центру мас визначається радіус-вектором
 ,
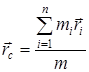| (7) |
де 
– радіус-вектори окремих матеріальних точок системи (рис. 2), а m – маса всієї системи:
 .
|
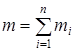Якщо (7) продиференціювати, отримаємо швидкість центру мас системи:
 ,
|
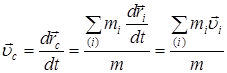де в чисельнику, згідно з (3), – імпульс системи 
. Звідси:
 .
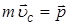| (8) |
Таким чином,
імпульс механічної системи дорівнює добутку її загальної маси на швидкість центру мас цієї системи.
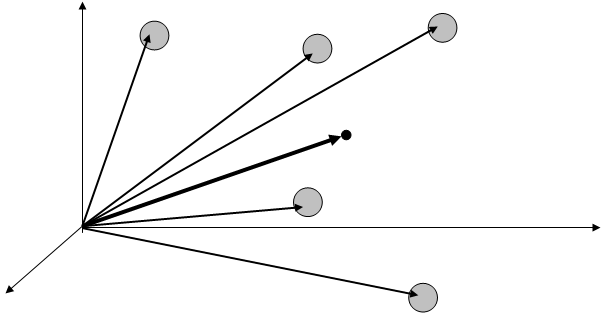z
m1 m2 m3
r1 r2 r3
ЦЕНТР МАС
rc
r4 m4
O r5 y
x m5
Рис. 2
Якщо (8) продиференціювати, то, враховуючи (4), отримаємо:
 .
| (9) |
Порівнюючи отримане співвідношення з ІІ законом Ньютона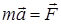 
, можна сказати, що
центр мас механічної системи рухається, як матеріальна точка, до якої прикладена рівнодіюча всіх зовнішніх сил, що діють на систему.
Цей висновок застосовується для спрощення математичного аналізу руху складних механічних систем. Такий рух можна розкласти на рух центру мас відносно зовнішньої системи відліку і рух частин системи відносно центру мас.
Прикладом такої системи є система Земля – Місяць, що рухається по еліптичній орбіті навколо Сонця. Згідно зі зробленим висновком, по еліптичній орбіті навколо Сонця рухається центр мас цієї системи. В свою чергу, Земля і Місяць обертаються навколо спільного центру мас. Таким чином, траєкторії їх руху є складним взаємонакладанням двох різних рухів.
2. Закон збереження енергії
На попередній лекції було визначено поняття повної механічної енергії системи, яка є сумою кінетичної і потенціальної енергій:
Е = Т + П.
Можна теоретично довести, що за відсутності дисипативних сил повна механічна енергія замкненої системи не змінюється з часом, відбувається лише перехід кінетичної енергії в потенціальну і навпаки. Таким чином, можна сформулювати закон збереження механічної енергії:
Не нашли, что искали? Воспользуйтесь поиском: