Дифференциальная ИКМ

Особенностью речевых сигналов, как и многих других источников информации, является то, что соседние значения отсчетов x_i очень похожи – близки по амплитуде друг к другу. В связи с этим можно попытаться предсказать значения текущего отсчета сигнала по нескольким предыдущим, и далее кодировать уже не значение самого отсчета, а ошибки его предсказания – разницы между истинным значением текущего отсчета и его предсказанным значением. Если точность предсказания достаточно высока, то ошибка предсказания очередного отсчета будет значительно меньше величины самого отсчета и для ее кодирования понадобится гораздо меньшее число бит. При этом, чем более предсказуемым будет поведение кодируемого сигнала, тем более эффективным будет его сжатие.

Эта идея лежит в основе так называемой дифференциальной импульсно-кодовой модуляции - ДИКМ (DPCM) – способа кодирования, при котором кодируется не само значение сигнала, а его отличие от предсказанных значений – ошибка предсказания .

Простейшим способом предсказания является использование предыдущего отсчета сигнала в качестве грубого предсказания его текущего значения:

= x_n-1 , = x_n - . (2.1)

Это так называемое предсказание нулевого порядка, самое простое, но и наименее точное. Ошибка предсказания в этом случае получается довольно большой, и для ее кодирования понадобится сравнительно много двоичных символов. Выигрыш, в сравнении с ИКМ будет небольшим (1-2 бита на отсчет).

Более точным, очевидно, будет предсказание текущего отсчета на основе линейной комбинации нескольких предшествующих:

= a _k x_{n – k}, = x_n - . (2.2)

В этом случае предсказанное значение текущего отсчета получается как взвешенная линейная комбинация нескольких предыдущих отсчетов x_n, где a _k - так называемые коэффициенты предсказания, - ошибка предсказания. Задача максимально эффективного кодирования состоит в выборе значений коэффициентов a _k.

Величины { a_k } должны выбираться таким образом, чтобы минимизировать некоторую функцию ошибки предсказания, например – средний квадрат различий между x_n и

ξ _p = < ² > = <(x_n - 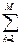a _k x_{n – k}) ² > =

< x_n² > - 2 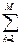_ka _k < x_n x_{n – k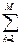} > + a _k a _l< x_n-l x_{n – k} >. (2.3)

Для стационарного сигнала { x_n } его статистические характеристики не зависят от времени, поэтому < x_n-l x_{n – k} > = <x_l x_k>, и выражение (2.3) запишется, как

ξ _p = R(0) – 2 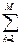a _k R(k) +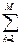 a _k a _l R(k-l), (2.4)

где R(k) - автокорреляционная функция последовательности отсчетов сигнала x_n, отражающая степень и характер связи между его различными отсчетами.

Чтобы минимизировать ξ _p по коэффициентам предсказания { a_k } нужно продифференцировать выражение 2.4 по a _k и приравнять производную к нулю. Это приводит к системе линейных уравнений вида:

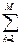a _k R(k-l) = R(l), l = 1,2,3 … M. (2.5)

Линейные уравнения (2.5) для коэффициентов предсказания называются нормальными уравнениями, или уравнениями Юли-Волкера.

Таким образом, оптимальные коэффициенты предсказания для ЛПК-кодера можно найти по автокорреляционной функции кодируемого сигнала. На основе найденных коэффициентов предсказания можно построить блок-схему ДИКМ кодера-декодера.

На рис. 3 и 4 приведены схемы кодера и декодера ДИКМ.

Рис. 3 Рис. 4

Благодаря существенному уменьшению динамического диапазона кодируемых данных (амплитуды ошибки предсказания в сравнении с исходным сигналом) ДИКМ обеспечивает выиг­рыш от 4 до 11 дБ по сравнению с ИКМ. Наибольший выигрыш достигается при переходе от системы без предсказания к предсказателю нулевого порядка, несколько мень­ший - при увеличении порядка от одного до 4 - 5, после чего вы­игрыш перестает увеличиваться. Увеличение от­ношения сигнал/шум означает, что системы с ДИКМ могут обес­печивать данное отношение сигнал/шум при разрядности, на 2 - 3 бита меньшей, чем это требовалось бы при прямом квантовании речевого сигнала.

При кодировании речевых сигналов с учетом их кратковременной корреляции (предсказуемости на несколько очередных отсчетов) результирующая скорость кода для ДИКМ (DPCM) в конечном итоге составляет 5 – 6 бит на отсчет или 40 – 48 кбит/с.

Дельта-модуляция (ДМ)

Дельта-модуляцию можно рассматривать как простейшую форму ДИКМ, в которой используется двухуровневый (1-битовый) квантователь и фиксированный предсказатель нулевого порядка.

При использовании ДМ текущее значение ошибки предсказания = x_n - кодируется и передается всего одним битом. Понятно, что для хорошей аппроксимации сигнал x(t) должен изменяться медленно в сравнении с частотой дискретизации. Поэтому, при использовании ДМ частоту дискретизации обычно выбирают в 5 - 6 раз большей, чем требуется по условиям Котельникова.

Блок-схема кодера-декодера ДМ приведена на рис. 5

Рис. 5

При заданной скорости дискретизации характеристики качества ДМ (величина ошибки предсказания = x_n - ) ограничены двумя видами искажений. Одно называется перегрузкой по крутизне, когда восстановленный сигнал при заданной величине шага квантования Δ “не успевает” за x(t), что требует увеличения Δ. Второй вид искажений – шум дробления, возникает на участках сигнала с малой или нулевой крутизной, и для своего снижения требует уменьшить Δ. Решение состоит в выборе компромиссного шага квантования или в адаптации шага квантования под скорость изменения кодируемого сигнала, подобной АДИКМ.

Дельта-модуляция из-за простоты кодирования и восстановления сигнала используется в простых цифровых системах передачи как речевых, так и других медленно меняющихся сигналов (в измерительных системах, в телеметрии и т.д.).

Цель работы: С использованием математического моделирования на ЭВМ и пакета MATLAB познакомиться с простейшими способами кодирования речевых сигналов – ИКМ, ДИКМ и ДМ. Изучить эффекты, возникающие при использовании этих методов кодирования.

Выполнение работы:

1. Сформировать и отобразить модель речевого сигнала, как стационарного случайного процесса с ограниченным спектром.

2. Сформировать и отобразить модель речевого сигнала, как последовательности вокализованного и невокализованного (гласного и согласного) звуков.

3. Отобразить спектры моделей речевого сигнала.

4. Исследовать кодирование этих сигналов с использованием ИКМ.

5. Выполнить квантование сигнала по уровню. Отобразить квантованный сигнал при различном (М = 2 …. 256) числе уровней квантования.

6. Декодировать ИКМ сигнал. Оценить характер и величину ошибок квантования от числа уровней квантования при ИКМ.

7. Построить зависимость уровня ошибок квантования и скорости кода ИКМ от числа уровней квантования.

8. Построить модель формирования ДИКМ нулевого порядка с предсказанием ВПЕРЕД.

9. Оценить характер и величину ошибки восстановления ДИКМ с учетом квантования ошибки предсказания при различном числе уровней квантования. Привести примеры для различного числа уровней квантования (М = 2 ….256).

10. Построить зависимость уровня ошибок квантования и скорости кода при ДИКМ от числа уровней квантования.

11. Построить модель ДИКМ нулевого порядка с предсказанием в цепи обратной связи. Оценить характер и величину ошибки восстановления ДИКМ с учетом квантования ошибки предсказания при различном числе уровней квантования (М= 2….32) для предсказания в цепи ОС.

12. Исследовать модель ДИКМ с квантованием ошибки на 2 уровня (δ-модуляция).

13. Исследовать влияние числа уровня квантования речового сигнала на субъективное качество его звучання. Использовать пример МАТЛАБ программы, приведенный в Приложении 2

14. Построить модель ИКМ-кодера в Simulink (Приложение 3). Отобразить средствами пакета кодируемый сигнал, дискретизованный и квантованный сигналы, а также ошибку квантования при различном числе уровней квантования.

15. Построить в Simulink модель ДИКМ-кодера с предсказанием нулевого порядка в цепи обратной связи, а также модель декодера.

16. Построить в Simulink модель кодера и декодера, использующего для работы данные из *.wav файла.

17. Подготовить в электронном виде отчет о выполненной работе.

Для выполнения работы можно использовать приведенные ниже примеры, внося в них необходимые дополнения и изменения.

Контрольные вопросы и задачи

1. Что такое “ квантование сигнала по уровню ” и как оно осуществляется?

2. Что такое “ погрешность квантования ” сигнала по уровню и как она определяется?

3. Из каких соображений выбирается количество уровней квантования сигнала?

4. Какой вид имеет распределение вероятностей шума квантования?

5. Что означает понятие “ разрядность АЦП ”?

6. Какими должны быть частота дискретизации и скорость кода ИКМ (бит/сек), обеспечивающие высокое качество кодирования речевого сигнала с полосой Fm = 4 кГц при равномерном квантовании?

7. Зачем используется неравномерное квантование при кодировании речи? Из каких соображений выбирается закон квантования?

8. Какова скорость кода ИКМ (бит/сек), обеспечивающая высокое качество кодирования речевого сигнала с полосой Fm = 4 кГц при логарифмическом квантовании?

9. Что такое ДИКМ? Изобразите схему кодирования и декодирования с использованием ДИКМ.

10. Что такое ЛПК? Из каких соображений выбираются коэффициенты предсказания при использовании ЛПК?

11. Что такое δ-модуляция? Изобразите схемы кодирования и декодирования с использованием ДМ.

12. Какие виды погрешностей характерны для ДМ и как их уменьшить?

Не нашли, что искали? Воспользуйтесь поиском: