Пояснения к решению задачи

Взаимно перпендикулярные плоскости π ₁, π _2, π ₃, называются плоскостями проекций, а линии их пересечения - координатными осями. Положение точки в пространстве вполне определяют две ее проекции.

Координаты точки, например А: Х_а, Y_a, Z_a, определяют расстояние от точки А до плоскости проекций π ₁, π _2, π ₃.

Проекция точки - точка пересечения проецирующей прямой, проходящей через данную точку, с плоскостью проекций.

Точка, например А, (рис. 2) имеет проекции А′, А″, А‴ которые называются:

А' - горизонтальная проекция;

А" - фронтальная проекция;

А‴- профильная проекция

Прямые АА′, АА», АА‴ называются проецирующими прямыми. Они проходят через точку А перпендикулярно соответствующей плоскости проекций (АА′ π ₁ - АА " - π ₂, АА‴ - π ₃.)

Чтобы получить плоский чертеж точки, поворачиваем плоскости проекций π ₁, (горизонтальную) и π ₃ (профильную) в указанном на рис. 3 направлении до совмещения с π ₂ фронтальной плоскостью проекций.

Рис. 2. Проекции точки

Полученный чертеж называют трехпроекционным комплексным чертежом точки (рис. 3).

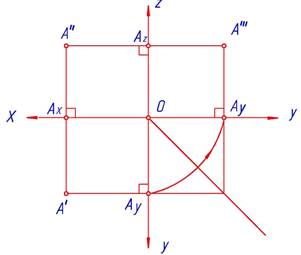
Рис. 3. Трехпроекционным комплексный чертеж

Проекцию точки на плоскость π ₃можно построить по двум ее известным проекциям на плоскости π ₁ и π _2, (рис.3.).

На комплексном чертеже ортогональные проекции точек А′ и А" и А‴ располагаются на прямых, перпендикулярных к соответствующим осям проекций.

Эти прямые (А’А ", А "А‴) называются линиями связи.

Для построения проекции прямой достаточно знать проекции двух ее несовпадающих точек.

Точка принадлежит прямой, если ее проекции принадлежат одноименным проекциям прямой. Справедливо и обратное утверждение. Например, если точка М принадлежит отрезку прямой АВ, то М'ϾА'В'; М"ϾА"В", М‴ϾА‴В‴

Ͼ- знак принадлежности.

Точка М, принадлежащая отрезку прямой АВ, удалена от плоскости проекций π₂ на таком расстоянии, на каком ее горизонтальная проекция удалена от оси X.

Точка М, принадлежащая отрезку прямой АВ, удалена от плоскости проекций π₁ на таком расстоянии, на каком удалена ее фронтальная проекция от оси X.

По комплексному чертежу отрезка прямой АВ можно определить положение точек А и В относительно друг друга, положение отрезка прямой в пространстве (рис. 4).

Точка А расположена: выше точки В, так как Z_А > Z_В', ближе к плоскости π₂, чем точка В, так как Y_А<Y_В', дальше от плоскости π₃, чем точка В, так как Х_А > Х_В.

Так как Z_А ≠ Z_В, Y_А ≠ Y_B и Ха ≠ Х_В то отрезок АВ не параллелен ни одной из плоскостей проекций, т.е. является отрезком прямой общего положения.

Рис.4. Проекции отрезка АВ

На плоскости проекций π₁ и π₂ он проецируется с искажениями.

Если Z_А = Z_В, то отрезок прямой параллелен плоскости π₁.

Такая прямая называется горизонталью (рис. 5).

На плоскость проекций π₁ отрезок АВ проецируется без искажения, к плоскости проекций π₂ наклонен под углом ɣ°.

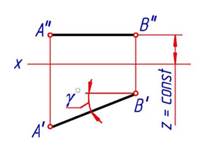
Рис. 5. Горизонталь	Рис.6. Фронталь

Такая прямая называется фронталью (рис. 6). На плоскость проекций π_2. отрезок CD проецируется без искажения, к плоскости проекций наклонен под углом φ°.

Прямая, параллельная двум плоскостям проекций, к третьей плоскости перпендикулярна и проецируется на нее в точку.

Прямая, перпендикулярная одной из плоскостей проекций, называется проецирующей.

Прямая, перпендикулярная горизонтальной плоскости проекций π ₁ называется горизонтально - проецирующей прямой (рис.7).

Прямая, перпендикулярная фронтальной плоскости проекций π ₂ называется фронтально - проецирующей прямой (рис.9).

Прямая, перпендикулярная профильной плоскости проекций π ₃ называется профильно - проецирующей прямой (рис.8).

Решение подобной задачи рассмотрено в [1, с. 14... 16; 2, с. 10...12; 4, с. 9...13].

Контрольные вопросы

1. Как на двухпроекционном комплексном чертеже определить расстояние от точки до плоскости π₁, до плоскости π _2.

2. Какая плоскость называется плоскостью проекций.

3. Какая прямая называется горизонталью, профильной линией и фронталью

4. Какие прямые называются горизонтально-, профильно- и фронтально-проецирующими прямыми.

5. При каких условиях проецируемые прямые будут перпендикулярны плоскостям проекций.

Рис. 7. Горизонтально проецирующая прямая	Рис.8. Профильно проецирующая прямая

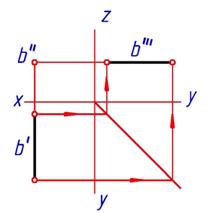
Рис. 9. Фронтально-проецирующая прямая

Задача 2

Задание. Определить натуральную величину отрезка АВ и угол его наклона к плоскости проекций π₁ (нечетные варианты) или к плоскости проекций π ₁ (четные варианты).

Координаты точек приведены в приложении 2.

Задачу решить двумя способами:

а) способом прямоугольного треугольника;

б) способом замены плоскостей проекций.

Не нашли, что искали? Воспользуйтесь поиском: