
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сечение пирамиды плоскостью.
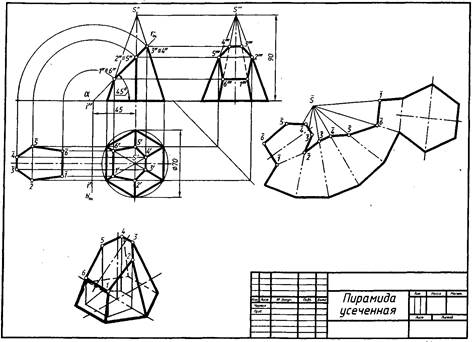
Правильная шестиугольная пирамида, пересеченная фронтально-проецирующей плоскостью α", показана на рисунке.
Фронтальная проекция сечения совпадает с фронтальным следом f 0α''плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости α " с ребрами пирамиды. Действительный вид фигуры сечения в этом примере найдем способом перемен плоскостей проекций.
Развертка боковой поверхности усеченной пирамиды с фигурой сечения и фигурой основания приведена на рисунке.
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку S0 (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки S'"E'" или S'"B'", так как эти ребра параллельны профильной плоскости и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например А0 откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок А'В'). Точки A0—E0 соединяют прямыми с вершиной S0. Затем от вершины S0 на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.

Рисунок 6.
На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — S'"5'" и S"2'". Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к горизонтальной плоскости и проходящей через вершину S.
Полученные точки 10, 20, 30 и т. д. соединяют прямыми и пристраивают фигуры основания и сечения. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
Построение изометрической проекции усеченной пирамиды начинают с построения изометрической проекции основания пирамиды по размерам, взятым с горизонтальной проекции комплексного чертежа.

Рисунок 7.
Затем на плоскости основания по координатам точек 1'—6' строят горизонтальную проекцию сечения (тонкие линии на основании пирамиды, рисунок 2).
 Рисунок 8.
Рисунок 8.
Из вершины полученного шестиугольника проводят вертикальные прямые, на которых откладывают координаты, взятые фронтальной или профильной проекции призмы, например, отрезки К1, К2, К3 и т. д. Полученные точки 1—6 соединяем, получаем фигу сечения. Соединив точки 1—6 с вершинами шестиугольника, основания пирамиды, получим изометрическую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.
Содержание работы. На листе чертежной бумаги формата A3 вычертить три проекции пирамиды. Провести фронтальный след секущей плоскости. Построить горизонтальную и профильную проекции фигуры сечения. Способом вращения вокруг выбранной оси построить действительный вид фигуры сечения. Построить развертку усеченной пирамиды. Построение изометрии усеченной пирамиды будет проводиться на занятиях совместно с преподавателем.
Условия работы даны в задании.
№1 №2 №3 №4




№5 №6 №7 №8




№ 9 № 10 № 11 № 12




№ 13 № 14 № 15 № 16
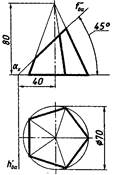
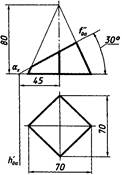


4. Перед решением задания №4 самостоятельно проработать темы: взаимное пересечение тел.
Не нашли, что искали? Воспользуйтесь поиском: