Постановка задачи ЛП, основные виды задач ЛП. Геометрическая интерпретация.

12 3 4 5 6 7 Следующая ⇒

Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

Виды задач:

1. Стандартная задача ЛП: 2. Каноническая задача ЛП:

Стандартная задача важна ввиду наличия большого числа прикладных моделей, сводящихся наиболее естественным образом к этому классу задач ЛП. Основные вычислительные схемы решения задач ЛП разработаны именно для канонической задачи.

3. Общая задача ЛП:

В этой задаче часть ограничений носит характер неравенств, а часть является уравнениями. Кроме того, не на все переменные наложено условие неотрицательности:

Здесь . Ясно, что стандартная задача получается как частный случай общей при 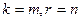; каноническая — при .

Все три перечисленные задачи эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных.

Линейная форма , подлежащая максимизации (или минимизации), называется целевой функцией.

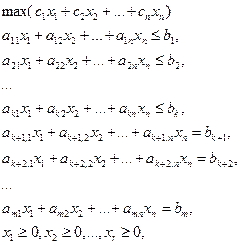
Геометрическая задача ЛП представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции линейное значение, причем допустимыми решениями служат все точки многогранника решений:

1)Построить множество допустимых пар(планов)

2) Нарм. … уровня целевой функции для нахождения максимума.

2. Понятия крайней точки и опорного плана. Теорема об оптимальности крайней точки.

Точка называется крайней (угловой) точкой выпуклого множества Х, если не существует точек , и числа таких, что .

Векторы x, y, z из называются линейно независимыми, если равенство 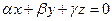. Возможно только в случае, когда все числа .

План называется опорным планом задачи

, если векторы входящие в разложение с положительными коэффициентами ( >0), линейно независимы.

Опорный план называется невырожденным, если он содержит ровно m положительных компонентов, в противном случае он назыв. вырожденным.

Теорема 2:

Если задача имеет решение, то максимальное значение линейной функции <c,x>= на выпуклом множестве допустимых планов X достигается хотя бы в одной из крайних точек множества X. Если максимальное значение целевая функция принимает в нескольких крайних точках, то она принимает его в любой точке, являющейся выпуклой комбинацией этих крайних точек.

3. Идея симплекс-метода. Признак оптимальности опорного плана, признак неограниченности целевой функции на множестве допустимых планов.

Идея с-м состоит в том, чтобы сначала попасть в крайнюю точку, затем проверить план на оптимальность. Если план оптимальный, то алгоритм работу закончил. Если план неоптимальный, то следует по ребру перейти в смежную крайнюю точку, в которой значение целевой функции будет лучше, чем в предыдущей. Затем нужно снова проверить полученный план на оптимальность. Таким образом, с-м будет двигаться от одной крайней точки к другой, последовательно улучшая значение целевой функции. Переходы будут закончены при достижении целевой функции оптимального значения.

Признак оптимальности:

Невырожденный опорный план задачи (4.3) и 4.4 оптимален тогда и только тогда, когда все оценки свободных переменных неотрицательны

Признак неограниченности:

Если в индексной строке с-таблицы задачи 4.3 и 4.4 содержится отрицательная оценка , а в соответствующем столбце переменной нет ни одного положительного элемента, то целевая функция не ограничена сверху на множестве допустимых планов.

12 3 4 5 6 7 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: