
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Системы уравнений появляются почти в каждой области прикладной математики. В некоторых случаях эти системы уравнений непосредственно составляют ту задачу, которую
необходимо решать, в других случаях задача сводится к такой системе. В практическом примере 10 мы увидим, например, что для проведения кривой, наилучшим образом соответствующей экспериментальным данным, приходится решать систему линейных уравнений, а в гл. 11 будут описаны методы решения уравнений в частных производных,
где также требуется решать системы алгебраических уравнений. Существует множество других задач, сводящихся к решению систем алгебраических уравнений.
В этой главе мы будем рассматривать системы из n уравнений с n неизвестными. Каждый член такого уравнения содержит только одно неизвестное, и каждое неизвестное входит только в первой степени. Такая система уравнений называется линейной, В случае двух неизвестных каждое уравнение графически изображается прямой линией, в случае трех неизвестных ему соответствует плоскость в трехмерном пространстве, а для четырех и более неизвестных — гиперплоскость. Искомое решение системы уравнений представляет собой набор значений неизвестных, удовлетворяющих одновременно всем уравнениям. Если задана некоторая произвольная система уравнений, то без предварительного исследования нельзя сказать, имеет ли она какое-либо решение и, в случае если решение существует, является ли оно единственным. На этот вопрос существуют три и только три ответа.
1. Решение системы уравнений существует и является единственным. Например,
 (1)
(1)
Решение этой системы х=1 и у=2, никакие другие значения х и у не способны одновременно удовлетворить

Рис. 1. Геометрическое представление системы двух линейных уравнений, имеющей единственное решение. Прямые линии, соответствующие уравнениям системы, образуют между собой довольно большой угол.
этим двум уравнениям. В этой главе мы будем в основном рассматривать именно такие системы уравнений, т. е. имеющие единственное решение. Геометрически эта система уравнений представлена на рис. 1, где видно, что две прямые линии, соответствующие двум уравнениям, пересекаются в одной и только в одной точке. Координаты этой точки как раз и представляют собой искомое решение.
2. Система уравнений вообще не имеет решения. Например,
 (2)
(2)
На рис. 2 показаны прямые линии, соответствующие этим двум уравнениям. Две прямые параллельны, они нигде не пересекаются, и система уравнений не имеет решения.

Рис. 2. Геометрическое представление системы двух линейных уравнений, не имеющей решения. Прямые линии параллельны.
3. Система уравнений имеет бесконечное множество решений. Например,
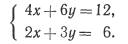
Как видно из рис. 8.3, эти два уравнения описывают одну и ту же прямую линию. Любая точка, лежащая на этой линии, является решением такой системы уравнений, например: х=0, у=2; х=1, у=4/3 и т. д.
Системы уравнений типа 2 и 3 называются вырожденными. Иногда непосредственно из поставленной задачи бывает ясно, что система уравнений не может быть вырожденной. Если же, как это бывает в большинстве случаев, соответствующая информация отсутствует, то приходится или проверять вырожденность системы уравнений в процессе решения, или исследовать такую возможность непосредственно. В разд. 8.2 мы увидим, что при решении системы уравнений методом Гаусса проверка вырожденности системы производится автоматически в процессе решения. Конечно,

Рис. 3. Геометрическое представление системы двух линейных уравнений, имеющей бесконечное множество решений. Оба уравнения изображаются одной и той же прямой линией.
непосредственная проверка состояла бы в вычислении определителя системы, тогда равенство определителя нулю прямо указывало бы на вырожденность. К сожалению, вычислить определитель ничуть не легче, чем просто решить систему уравнений.
С точки зрения обычной математики система линейных уравнений всегда является или вырожденной, или невырожденной. С точки же зрения практических вычислений могут существовать почти вырожденные системы, при решении которых получаются недостоверные значения неизвестных.
Рассмотрим систему уравнений:
 (3)
(3)
Эта система имеет единственное решение х=1, у=1. Теперь рассмотрим пару значений неизвестных х=2.415, y=0. При подстановке этих значений в исходные уравнения получаем
 (4)
(4)
После округления до двух значащих цифр правые части равенств (4) совпадают с правыми частями исходных уравнений. А так как исходные уравнения были заданы

Рис..4. Геометрическое представление системы двух линейных уравнений, которая является почти вырожденной. Прямые, соответствующие двум уравнениям, почти совпадают.
только с точностью до двух значащих цифр, то решение (4) так же хорошо отвечает условиям поставленной задачи, как и решение х = 1, у = 1.
Дело в том, что две прямые линии, описываемые двумя уравнениями этой системы, почти параллельны, как это показано на рис. 4. Точка х = 2.415, у = 0 хотя и не лежит ни на одной из этих прямых линий, но очень близка к ним.
Системы типа (3) называются плохо обусловленными. В любом случае, когда две линии (либо плоскости и гиперплоскости) почти параллельны, система уравнений становится плохо обусловленной. В этом случае найти численное решение системы трудно, а точность его весьма сомнительна. Более того, система из трех и более уравнений может оказаться плохо обусловленной, даже если никакие плоскости не являются параллельными или почти параллельными[1]. Вне зависимости от геометрической интерпретации обусловленность системы можно исследовать при ее решении методом Гаусса или с помощью специальной проверки.
Перед тем как переходить к подробному рассмотрению методов решения системы уравнений, остановимся вкратце на двух основных направлениях в этой области.
Методы численного решения системы линейных уравнений подразделяются на два типа, прямые (конечные) и итерационные (бесконечные). Первая группа методов рассматривается в разд. 8.2, вторая — в разд. 8.6. Естественно, никакой практический метод решения системы уравнений не может быть бесконечным. Мы имеем в виду только то, что прямые методы могут в принципе (с точностью до ошибок округления) дать точное решение, если оно существует, с помощью конечного числа арифметических операций. С другой стороны, итерационный метод требует бесконечного числа арифметических операций, приводящих к точному решению. Иными словами, при использовании итерационного метода появляется ошибка ограничения, отсутствующая в прямых методах.
Из сказанного выше вовсе не следует, что решение, полученное с помощью прямого метода, обязательно будет точнее, так как ошибка округления играет большую роль. При решении большой плохо обусловленной системы прямым методом ошибки округления могут привести к бессмысленным результатам. Несмотря на неизбежную ошибку ограничения, итерационный метод может оказаться наиболее удобным, так как при его использовании ошибки округления не накапливаются.
После разбора обоих методов решения систем линейных уравнений мы кратко сравним их и проанализируем ошибки. Мы увидим, что оба метода полезны и удобны для практических вычислений, а каждый из них имеет свои преимущества и недостатки.
МЕТОД ИСКЛЮЧЕНИЯ (МЕТОД ГАУССА)
В этом разделе мы рассмотрим один из наиболее известных и широко применяемых прямых методов решения систем линейных уравнений. Обычно этот метод называют методом исключения или методом Гаусса.
Чтобы проиллюстрировать этот метод, рассмотрим сначала систему из трех уравнений с тремя неизвестными:
 (5) (6) (7)
(5) (6) (7)
В такой системе по крайней мере один из коэффициентов а11, a21, а31 должен быть отличен от нуля, иначе мы имели бы дело в этих трех уравнениях только с двумя неизвестными. Если a11=0, то можно переставить уравнения так, чтобы коэффициент при x1 в первом уравнении был отличен от нуля. Очевидно, что перестановка уравнений оставляет систему неизменной: ее решение остается прежним.
Теперь введем множитель

Умножим первое уравнение системы (5) на m2 и вычтем его из уравнения (6). («Первое» и «второе» уравнения мы берем уже после перестановки, если она была необходима.) Результат вычитания равен
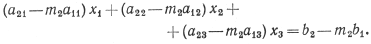 (8)
(8)
Но ведь
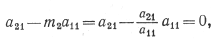
так что x1 исключено из второго уравнения (конечно, именно для достижения такого результата и было выбрано значение m2). Определим теперь новые коэффициенты
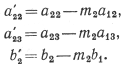
Тогда уравнение (8.6) приобретает вид
 (9)
(9)
Заменим второе из первоначальных уравнений (6) уравнением (9) и введем множитель для третьего уравнения

Умножим первое уравнение на этот множитель и вычтем его из третьего. Коэффициент при xt снова становится нулевым, и третье уравнение приобретает вид
 (10)
(10)
где
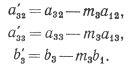
Если теперь в исходной системе уравнений заменить (7) на (10), то новая система выглядит так:
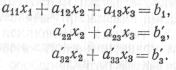 (5)(9)(10)
(5)(9)(10)
Эти новые уравнения полностью эквивалентны исходным уравнениям с тем преимуществом, что x1 входит только в первое уравнение и не входит ни во второе, ни в третье. Таким образом, два последних уравнения представляют собой систему из двух уравнений с двумя неизвестными; если теперь найти решение этой системы, т. е. определить x2 и x3, то результат можно подставить в первое уравнение и найти x1. Иначе говоря, задача сведена к решению системы из двух уравнений с двумя неизвестными.
Попытаемся теперь исключить х2 из двух последних уравнений. Если а'22=0, то снова мы переставим уравнения так, чтобы a22 было отлично от нуля. (Если же а'22=0 и a'32=0, то система вырождена и либо вовсе не имеет решения, либо имеет бесчисленное множество решений.) Введем новый множитель
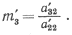
Умножим уравнение (9) на m '3 и вычтем его из (10). Результат вычитания равен
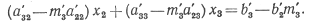
В силу выбора т'3

Полагая

окончательно получаем
 (11)
(11)
Уравнение (8.10) можно заменить уравнением (11), после чего система уравнений приобретает следующий вид:
 (5)(9)(11)
(5)(9)(11)
Такая система уравнений иногда называется треугольной из-за своего внешнего вида.
Теперь совершенно очевидно, что надо делать для решения системы. Необходимо определить х3 из (11), подставить этот результат в (9), определить х2 из (9), подставить х3 и х2 в (5) и определить x1. Этот процесс, который обычно называется обратной подстановкой, определяется в нашем случае формулами

Вспомним, что мы всегда переставляли уравнения таким образом, чтобы аи и а'22 не были равны нулю. Если же окажется, что а''33 = 0, то система уравнений вырождена.
Рассмотрим пример
 (12)
(12)
Легко убедиться, что множители для второго и третьего уравнений равны соответственно 2 и 1. После исключения x из второго и из третьего уравнений новый множитель, исключающий y из третьего уравнения, равен —2. Треугольная система уравнений имеет вид
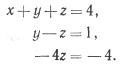
Из последнего уравнения z = 1, из второго у = 2, из первого x = 1. Можно подставить эти значения в исходные уравнения и убедиться, что они точно удовлетворяются. Таким образом, мы нашли точное решение системы с помощью конечного числа арифметических операций. В данном случае ошибки округления отсутствовали.
Теперь можно обобщить этот метод на случай системы из n уравнений с n неизвестными. После «алгебраического» описания алгоритма мы рассмотрим блок-схему программы, которая увеличивает наглядность алгоритма и позволяет непосредственно составить программу для вычислений на ЭЦВМ.
Обозначим неизвестные через x1, x2,..., хn и запишем систему уравнений в следующем виде:
 (13)
(13)
Предполагается, что в силу расположения уравнений a11 не равно нулю. Введем n-1 множителей

и вычтем из каждого i-гo уравнения первое, помноженное на mi. Обозначая

легко убедиться в том, что для всех уравнений, начиная со второго,

Преобразованная система уравнений запишется в следующем виде:
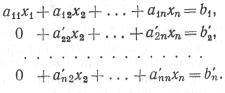
Продолжая таким же образом, мы можем исключить х2 из последних n-2 уравнений, затем х3 из последних п- 3 уравнений и т. д. На некотором k-u этапе мы исключаем xk c помощью множителей
 (14)
(14)
причем предполагается, что  не равно нулю. Тогда
не равно нулю. Тогда
 (15) (16)
(15) (16)
для i=k+1,...,n и для j=k,...,n. Индекс k принимает последовательные целые значения от 1 до n-1 включительно. При k=n-1 происходит исключение хn-1 из последнего уравнения.
Окончательная треугольная система уравнений записывается следующим образом:
 (17)
(17)
Блок-схема программы для процесса исключения неизвестных приведена на рис. 8.5. Эта блок-схема точно соответствует разобранному выше алгебраическому процессу с двумя принципиальными различиями. Прямоугольник, где написано «переставить уравнения так, чтобы akk ≠0», означает некоторый алгоритм, описанный в разд. 8.3 после разбора ошибок округления. Мы увидим, что ошибки округления могут быть существенно уменьшены, если следовать определенным правилам перестановки уравнений.
Второе различие сводится к тому, что в блок-схеме все множители обозначаются одним и тем же символом m. В самом деле, если вычисления в программе правильно организованы, то на каждом определенном этапе вычислений не требуется больше одного множителя.
При анализе блок-схемы полезно четко представлять себе смысл индексов i, j и k:
k означает номер того уравнения, которое вычитается из остальных, а также номер того неизвестного, которое исключается из оставшихся n-k уравнений.
i означает номер уравнения, из которого в данный момент исключается неизвестное.
j означает номер столбца.
Мы рекомендуем тщательно проанализировать блок-схему, приведенную на рис. 5. Она не только позволяет ясно представить себе метод исключения, но также иллюстрирует некоторые полезные приемы, применяемые при написании блок-схемы, в частности использование индексов.
Полезно заметить, что процесс исключения неизвестных не изменяет абсолютной величины определителя системы, хотя знак определителя и изменяется при каждой перестановке уравнений. После окончания процесса значение определителя равно произведению диагональных элементов, причем знак этого произведения надо изменить на обратный,

Рис. 5. Блок-схема программы для решения системы линейных уравнений методом исключения.
если количество перестановок было нечетным. Таким образом, значение определителя системы удобно вычислять именно с помощью метода исключения.
Обратная подстановка для нахождения значений неизвестных задается формулами
 (18)
(18)
Блок-схема программы для обратной подстановки приведена на рис. 6. Она существенно проще блок-схемы метода исключения. Оказывается также, что эта блок-схема еще упрощается, если вычислять значение xn в начале программы, не включая это вычисление в цикл. Конечно, можно составить блок-схему и без этого отдельного шага, но при этом ненужным образом усложнилось бы вычисление суммы членов, стоящих после диагонального: первая «сумма» оказалась бы равной нулю и проверку индекса j пришлось бы производить перед вычислением суммы. Заметим, что, если в блок-схеме на рис. 8.5 все индексы в процессе вычисления увеличивались, в блок-схеме на рис. 8.6 один из индексов, а именно i, уменьшается.
ОШИБКИ ОКРУГЛЕНИЯ
В этом разделе мы рассмотрим ошибки округления, которые возникают при вычислениях с плавающей запятой. Здесь мы зададимся целью не столько найти верхнюю границу возможной ошибки округления (хотя эту верхнюю границу и можно определить), сколько указать правило организации вычислений, которое свело бы ее к минимуму. Определение величины самой ошибки отложим до разд. 8.4, где будет рассмотрен метод, позволяющий использовать ЭЦВМ не только для определения величины ошибки, но и для коррекции ошибочных результатов.
Вспомним, что перед началом процесса исключения очередного неизвестного может понадобиться переставить уравнения в системе, чтобы избежать деления на нуль. Обычно приходится делать несколько таких перестановок. В этом разделе мы покажем, как с помощью соответствующего выбора пары уравнений для перестановки можно существенно уменьшить ошибки округления. Оказывается, что обычно перестановка уравнений желательна, даже если диагональный член и не равен нулю.
Предположим, что мы собираемся исключить хk. Система уравнений имеет следующий вид:


Рис. 6. Блок-схема программы для обратной подстановки при решении системы уравнений методом исключения.
[1] Представьте себе три параллельные линии, проходящие через три вершины треугольника и перпендикулярные к его плоскости. Теперь проведите плоскость через каждую пару параллельных линий. Эти три плоскости не параллельны, но они нигде не пересекаются в одной точке. Если же одна из плоскостей слегка наклонена, то три плоскости пересекутся в одной точке, но система уравнений будет плохо обусловленной.
| <== предыдущая лекция | | | следующая лекция ==> |
| УСОВЕРШЕНСТВОВАННЫЙ МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ | | | МЕТОД НЬЮТОНА — РАФСОНА |
Не нашли, что искали? Воспользуйтесь поиском: