Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)

В ряде приложений приходится решать систему линейных алгебраических уравнений с матрицей, у которой равны нулю все элементы, кроме элементов, расположенных на главной диагонали, на диагоналях, расположенной над и под главной диагональю. Такие системы уравнений называются трехдиагональными. Трехдиагональная система уравнений может быть решена методом Гаусса. Однако в этом случае метод Гаусса упрощается. Метод гаусса, модифицированный для решения трехдиагональных систем линейных алгебраических уравнений, получил название метода прогонки. Изложим его.

Трехдиагональная СЛАУ имеет следующий вид:

.

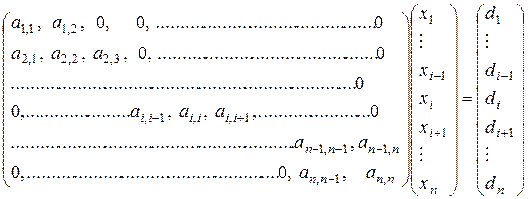Эту системы уравнений можно записать в виде

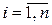, , (9.19)

, .

Удобнее для обозначения коэффициентов СЛАУ использовать один индекс. Обозначив

,

,

,

,

вместо (9.19) получим

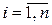, , (9.20)

, .

Формула (9.20) представляет собой разностное уравнение. Применяя к трехдиагональной системе (9.20) метод Гаусса, замечаем, что прямой ход метода сводится к исключению элементов . После окончания прямого хода получается система уравнений, содержащая в каждом 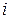-м уравнении только 2 неизвестных: и 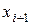. Поэтому формулы обратного хода имеют вид

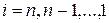, , (9.21)

где 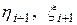– некоторые числа.

Получим на основании формулы (9.21) формулы прямого хода. Для этого уменьшим в (9.21) индекс 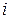на единицу,

, (9.22)

и подставим (9.21) и (9.22) в уравнение (9.20). Получим

.

Выражая отсюда , будем иметь

. (9.23)

Чтобы выражение (9.23) совпало с (9.21), необходимо выполнение равенств

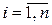, , . (9.24)

Формулы (9.24) – это формулы прямого хода метода прогонки, а формула (9.21) – обратного хода. Осталось определить, с каких значений начинать расчеты по формулам прямого и обратного хода. Расчеты прямого хода по формуле (9.24) начинаются со значени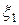й и , которые нам неизвестны. Однако в формулах (9.24) перед 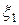и стоит множитель , который равен нулю. Поэтому можно брать 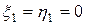. Расчеты обратного хода по формуле (9.21) начинаются со значения . Поскольку перед в (9.21) стоит множитель 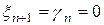, то следует взять .

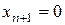Вычисления по формулам (9.21), (9.24) метода прогонки требуют всего 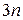ячеек памяти и арифметических операций, что гораздо меньше, чем по общим формулам метода исключения Гаусса.

Попутно с решением системы уравнений можно найти определитель трехдиагональной матрицы системы уравнений по формуле

.

Не нашли, что искали? Воспользуйтесь поиском: