Энергия бегущей волны. Вектор плотности потока энергии

Упругая среда, в которой распространяется волна, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией среды. Можно показать, что объемная плотность энергии для плоской бегущей гармонической волны (5)

, (15)

где r=dm/dV – плотность среды, т.е. периодически изменяется от 0 до rА²w² за время p/w=Т/ 2.

Среднее значение плотности энергии за промежуток времени p/w=Т/ 2

. (16)

Для характеристики переноса энергии вводят понятие вектора плотности потока энергии – вектор Умова.

Выведем выражение для него.

Если через площадку DS _^, перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии

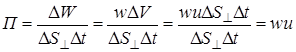, (17)

где DV=DS _^ uDt – объем элементарного цилиндра, выделенного в среде.

Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора

, Вт/м². (18)

Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г.

Среднее значение его модуля называют интенсивностью волны

. (19)

Для гармонической волны u =v [cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v.

Стоячие волны

Если навстречу друг другу распространяются две гармонические волны и , то образуется стоячая волна

. (20)

Исследуем сначала множитель cos kx= cos2 px/l. В точках x= ±(1+2 n) l/ 4, где n =0,1,2..., cos kx= 0 и, следовательно, S= 0. Эти точки не колеблются и поэтому называются узлами стоячей волны (см. рис.3). Расстояние между соседними узлами равно l/ 2. Точки максимальной амплитуды стоячей волны называются пучностями. Их координаты x= ± nl/ 2. Расстояние между соседними пучностями равно l/ 2.

На рис. 3 сплошной линией изображена зависимость от х, соответствующая моменту времени t (например, t= 0), при котором cos wt= cos2 pt/T =1. Через четверть периода cos 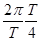=0 и S =0. Еще через время, равное T/ 4, cos = -1, и соответствующая зависимость S от х изображена штриховой линией (см. рис. 3). Спустя t= 3 T/ 4 S =0 и через t=T все повторится.

В случае стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут энергию в противоположных направлениях. Т.о., стоячая волна характеризует колебательное состояние среды.

В заключении отметим, что несмотря на разнообразие волновых явлений, они описываются одинаковыми законами (математичеcкими уравнениями). Это позволяет, например, перенести полученные в данной лекции закономерности для упругих волн на электромагнитные волны.

Лекция 2. Электромагнитные волны

Во второй части курса физики изучались уравнения Максвелла, которые в дифференциальной форме (т.е. справедливые для бесконечно малого объема среды) имели вид:

(1)

где и – векторы напряженности электрического и магнитного полей, которые измеряются соответственно в В/м и А/м; – вектор магнитной индукции (Тл), – вектор электрического смещения (Кл/м²), – вектор плотности тока проводимости (А/м²), r – объемная плотность заряда (Кл/м³).

Кроме того, необходимо учитывать, что

(2)

где e₀ =1/(4p×9×10⁹) Ф/м, m₀ =4p×10^-7 Гн/м – электрическая и магнитная постоянные; ε, μ – диэлектрическая и магнитная проницаемости среды; g – удельная электропроводность среды (величина, обратная удельному сопротивлению), а также, что

, (3)

c – скорость света в вакууме, с = 3×10⁸ м/с.

Скорость распространения электромагнитных волн в среде

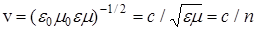, (4)

где , (5)

n – абсолютный показатель преломления среды, он показывает, во сколько раз скорость света v в среде меньше скорости света в вакууме с.

Из первого уравнения Максвелла следует, что переменное (изменяющееся во времени) магнитное поле вызывает переменное электрическое поле, а оно [согласно второму уравнению (1)], изменяясь, вызывает магнитное поле и т.д. Нельзя создать только электрическое поле, не вызвав магнитного поля и наоборот. Т.е. электрическое и магнитное поля взаимосвязаны. Они образуют единое электромагнитное поле, которое распространяется в пространстве (среде) в виде электромагнитных волн.

Волновые уравнения

Электромагнитные волны удовлетворяют уравнениям аналогичным (1.9)*, которые выводятся из уравнений Максвелла с применением векторного равенства

Для линейной однородной изотропной среды при отсутствии токов () и зарядов (r =0) волновые уравнения для векторов и имеют вид

, , (6)

где и – операторы Лапласа, примененные к векторам и соответственно, они выражаются через операторы Лапласа от скалярных функций

(7)

где – единичные векторы (орты).

В (1.10) приведено выражение для оператора Лапласа, примененного к скалярной функции. Будем далее предполагать, что электромагнитная волна распространяется в направлении оси x (см. рис. 1) со скоростью и при этом вектор колеблется в одной плоскости, например, в плоскости xoy (эту плоскость называют плоскостью поляризации). Тогда вектор будет колебаться в перпендикулярной к ней плоскости xoz [это следует из двух первых уравнений (1)], т.е. в такой линейно поляризованной волне векторы и имеют только по одной составляющей, т.е. .

Следует заметить, что векторы , и образуют правую тройку взаимноперпендикулярных векторов (т.е. направление вектора совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от к по наикратчайшему пути).

Для такой линейно поляризованной волны волновые уравнения (6) упростятся и примут вид

, , (8)

где индексы y и z при Е и Н подчеркивают лишь то, что векторы и направлены вдоль взаимно перпендикулярных осей y и z.

Не нашли, что искали? Воспользуйтесь поиском: