ЛАБОРАТОРНА РОБОТА № 3

КРИПТОГРАФІЯ З ВІДКРИТИМ КЛЮЧЕМ. ФУНКЦІЯ ҐЕШУВАННЯ

Мета роботи: ознайомитися з найпростішою функцією ґешування та схемами електронного цифрового підпису RSA та ElGamal.

Використовуване програмне забезпечення: пакети математичних обчислень MathCad і Maple.

3.1 Теоретичні відомості

3.1.1 Асиметричні криптосистеми

Ефективними системами криптографічного захисту даних є асиметричні криптосистеми. В таких системах для зашифрування даних використовується один ключ, а для розшифрування – інший. Причому ключі пов’язані між собою певним математичним співвідношенням, що робить можливим процес адекватного розшифрування. Концепція таких криптосистем основана на застосуванні однонаправлених функцій з секретом, що дозволяє легко отримати відкритий ключ із секретного, але не навпаки.

Двухключова криптографія використовується в двух схемах: цифрового підпису і спрямованого шифрування. В першому випадку повідомлення підписується закритим ключем і будь-яка особа може упевнитися в його дійсності за допомогою відкритого ключа. В схемі спрямованого шифрування, навпаки, повідомлення зашифровується на відкритому ключі отримувача. Розшифрувати повідомлення має можливість тільки сам отримувач за допомогою свого секретного ключа.

В протоколах цифрового підпису застосовується так звана «ґеш-функція».

Ґеш-функціей називається перетворення H, що переводить повідомлення M довільної довжини у повідомлення H(M) фіксованої довжини. Ґеш-функція повинна задовольняти таким вимогам:

- не вище чим поліноміальна складність обчислення значення ґеш-функції;

- не нижче чим експоненціальна складність визначення повідомлення Mi по відомому значенню H(Mi);

- практична захищеність від колізій, коли можна знайти Mi та Mj, такі, що H(Mi) = H(Mj), з імовірністю не вище чим Pk, де Pk завідомо задане значення.

3.1.2 Алгоритм RSA в схемі спрямованого шифрування

Алгоритм RSA запропонували у 1978 р. три автора Р.Райвест, А.Шамір, А.Адлеман. Стійкість алгоритму базується на складності факторизації великих чисел і трудності обчислення дискретних логарифмів.

Алгоритм RSA використовується в моделі взаємної недовіри. Її сутність полягає в тім, що кожен користувач генерує ключі сам собі. Особистий ключ залишає в себе і забезпечує його строгу конфіденційність. Відкритий ключ розсилає всім користувачам, з якими він зв'язаний. Він також забезпечує цілісність і дійсність відкритих ключів. Таким чином, будь-хто може надіслати йому повідомлення, зашифроване на відомому відкритому ключі, яке може прочитати тільки сам користувач, бо тільки він володіє відповідним секретним ключем.

Алгоритм 3.1

1. Обираємо модуль перетворень N=P*Q, де P, Q – випадкові великі прості числа.

2. Обчислюємо , де - функція Ейлера, що вказує кількість додатних цілих чисел в інтервалі від 1 до N, що взаємно прості з N.

3. Відкритий ключ e вибирається випадково так, щоб виконувались умови

4. Обчислюємо закритий ключ d з умови

,

використовуючи розширений алгоритм Евкліда. Ключ d та модуль N повинні бути взаємно простими.

5. Зашифрування повідомлення M відбувається за формулою

6. Розшифрування повідомлення відбувається за формулою

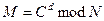
3.1.3 Цифровий підпис Эль-Гамаля

Цифровий підпис Эль-Гамаля базується на великій обчислювальній складності задачі дискретного логарифмування.

Позначення:

p – велике просте число, модуль перетворень;

a – первісний корінь за модулем p;

x – секретний ключ;

y – відкритий ключ ;

M – повідомлення, що підписується (M<p);

r, s = f(M,x) – підпис.

Алгоритм 3.2

Формування підпису Эль-Гамаля

1. Згенерувати випадкове число k, що задовольняє умовам

0<k<p-1 и НОД(k,p-1)=1

1. Обчислити r=a^k(mod p)
2. Обчислити s з рівняння

M=xr+ks (mod(p-1))

З теорії чисел відомо, що таке рівняння має рішення для s, якщо НОД(k,p-1)=1.

Перевірка підпису Эль-Гамаля.

Якщо (a^M)=a^xra^ks=y^rr^s (mod p) підпис є дійсним.

Не нашли, что искали? Воспользуйтесь поиском: