ЛАБОРАТОРНА РОБОТА № 4

КРИПТОГРАФІЧНІ ПЕРЕТВОРЕННЯ НА ЕЛІПТИЧНИХ КРИВИХ

Мета роботи: ознайомитися з алгоритмами криптографічних перетворень на еліптичних кривих.

Використовуване програмне забезпечення: пакет математичних обчислень Maple.

4.1 Теоретичні відомості

На даний час на території України діють:

а) закон України ”Про електронний цифровий підпис” – 2003, що визначає правовий статус електронного цифрового підпису та регулює відносини, що виникають при використанні електронного цифрового підпису;

б) закон України ”Про електронні документи та електронний документообіг” – 2003, що встановлює основні організаційно-правові положення електронного документообігу та використання електронних документів.

Сучасні світові стандарти цифрового підпису ґрунтуються на арифметиці еліптичних кривих. Наприклад:

ДСТУ 4145-2002. Державний стандарт України. Інформаційні технології. Криптографічний захист інформації. Цифровий підпис, що ґрунтується на еліптичних кривих. Формування та перевірка. Київ:-Держстандарт України, 2003.

ГОСТ Р 34.10-2001. Государственный стандарт российской федерации. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки цифровой подписи. М.: Госстандарт России, 2001.

ANSI X9.62. Public Key Cryptography for the Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA), 1999.

Еліптична крива - це математичний об'єкт, що може бути визначений над будь-яким полем, зокрема над полем дійсних чисел або над скінченним полем Галуа.

У загальному випадку еліптична крива над полем К має вигляд

E: y ² + axy + by = x ³ + cx ² + dx + e,

де a, b, c, d, e Î K.

На рис.4.1 поданий приклад еліптичної кривої, визначеної рівнянням

y ² = x ³ + x + 1,

над полем дійсних чисел R.

Рисунок 4.1 - Приклад еліптичної кривої y ² = x ³ + x + 1 над R.

4.1.1 Еліптичні криві над простим полем Галуа GF (p)

У криптографії застосовуються еліптичні криві, визначені над скінченнимим полями Галуа GF (q). У цьому випадку вони являють собою множину точок E (GF (q)), координати яких задовольняють рівнянню кривої.

Приклад. Дано еліптичну криву y² = x³ + x + 1(mod 5) над полем GF (5). Цьому рівнянню задовольняють 8 скінченних точок із координатами з GF (5). На рис.4.2 подано приклад цієї кривої.

Рисунок 4.2 - Приклад еліптичної кривої y ² = x ³ + x + 1 mod 5 над полем GF (5)

Розглянемо еліптичні криві над простим полем GF (p):

y ² = x ³ + ax + b (mod p), (4.1)

де р - просте число - модуль перетворень; параметри кривої
a, b Î GF (p) - невід¢ємні і задовольняють умові гладкості кривої , змінні x, y Î GF (p).

Крім точок (x, y), що задовольняють рівнянню (4.1), у множину точок еліптичної кривої також включається нескінченно віддалена точка O.

Наприклад, при p = 2 точками еліптичної кривої
y² = x³ + x +1 (mod 2) є три точки - (0,1), (1,1) і O.

Позначимо через E_p (a, b) множину точок еліптичної кривої виду (4.1).

На множині E _p(a, b) введемо операцію додавання + за правилом: нехай P ₁=(x ₁, y ₁) і P ₂=(x ₂, y ₂) – точки еліптичної кривої, тоді координати суми точок P ₃ = P ₁+ P ₂ = (x ₃, y ₃) визначаються за формулами

x ₃ = (l ² – x ₁ – x ₂) mod p

y ₃ = (l (x ₁ – x ₃) – y ₁) mod p

Якщо P ₁¹ P ₂, то .

Якщо P ₁= P ₂, то .

Вважаємо, що P + O = O + P.

Твердження. Множина точок еліптичної кривої E_p (a, b) з операцією додавання + утворює адитивну абелеву групу з нейтральним (нульовим) елементом O, тобто виконуються умови групи:

а) якщо P і Q Î E _p(a, b), то P + Q Î E _p(a, b);

б) для будь-яких трьох точок кривої P, Q, S Î E _p(a, b)

P + (Q + S) = (P + Q) + S;

в) для будь-якої точки P = (x, y) Î E _p(a, b) існує обернена точка – P, така, що P + (– P) = O; точка (– P) має координати (x, – y).

Приклад. Знайдемо точки еліптичної кривої y ² = x ³ + x + 1(mod 5). Можливі значення змінної x Î {0, 1, 2, 3, 4}. Задаючи значення x, знайдемо y:

x = 0 y ² = 1 Þ y = 1, y = – 1 або y = 4

x = 1 y ² = 3 Þ розв'язків немає

x = 2 y ² = 11 = 1 Þ y = 1, y = 4

x = 3 y ² = 31 = 1 Þ y = 1, y = 4

x = 4 y ² = 69 = 4 Þ y = 2, y = – 2 або y = 3

Таким чином, одержимо точки (0,1), (0,4), (2,1), (2,4), (3, 1), (3,4), (4,2), (4,3) і добавляємо точку O. Еліптична крива E₅ (1,1) містить 9 точок.

Визначення. Порядком групи точок еліптичної кривої E_p (a, b) називається число елементів цієї групи. Позначення - # E_p (a, b).

Група точок еліптичної кривої E₅ (1,1) має порядок рівний 9.

4.1.2 Алгоритм обчислення точок еліптичної кривої

Нехай задана еліптична крива y ² = x ³ + ax + b (mod p). Для кожного значення x, 0 £ x £ p – 1:

а) обчислюємо A = x ³ + ax + b (mod p);

б) вирішуємо порівняння y ²=A (mod p). Якщо порівняння має розв'язок, то є два значення y (крім випадку y = 0) – y ₁, y ₂:
y _i² =A (mod p). У цьому випадку точки (x, y ₁) і (x, y ₂) належать еліптичній кривій.

4.1.3 Приклад додавання точок еліптичної кривої y² = x³ + x + 1(mod 5).

Нехай P ₁ = (0,1), P ₂ = (4,2), x ₁ = 0, y ₁ = 1, x ₂ = 4, y ₂ = 2.

а) P ₁ + P ₂ = (x ₃, y ₃).

Так як P ₁ ¹ P ₂, то ,

l = (2-1)/(4-0) = ¼ mod 5 = 4.

x ₃ = (l ² – x ₁ – x ₂) mod p = 16 – 0 – 4 = 12 mod 5 = 2.

y ₃ = (l (x ₁ – x ₃) – y ₁) mod p = 4 (0 – 2) – 1 = – 9 mod 5 = 1.

Таким чином, (0,1) + (4,2) = (2,1).

b) 2 P ₁ = (x ₃, y ₃)

Так як P ₁ = P ₂, то ,

l = (3×0 + 1)/(2×1) = 1/2 mod 5 = 3.

x ₃ = (l ² – x ₁ – x ₂) mod p = 9 – 0 – 0 = 9 mod 5 = 4.

y ₃ = (l (x ₁ – x ₃) – y ₁) mod p = 3 (0 – 4) – 1 = – 13 mod 5 = 2.

Таким чином, 2×(0,1) = (4,2).

c) Аналогічно можна обчислити

3 P ₁ = 2 P ₁ + P ₁ = (4,2) + (0,1) = (2,1)

4 P ₁ = 3 P ₁ + P ₁ = (2,1) + (0,1) = (3,4)

5 P ₁ = 4 P ₁ + P ₁ = (3,4) + (0,1) = (3,1)

6 P ₁ = 5 P ₁ + P ₁ = (3,1) + (0,1) = (2,4)

7 P ₁ = 6 P ₁ + P ₁ = (2,4) + (0,1) = (4,3)

8 P ₁ = 7 P ₁ + P ₁ = (4,3) + (0,1) = (0,4)

9 P ₁ = 8 P ₁ + P ₁ = (0,4) + (0,1) = O

Визначення. Точка P Î E_p (a, b) називається базовою точкою підгрупи точок еліптичної кривої E_p (a, b), якщо будь-яка точка Q цієї підгрупи може бути подана у вигляді Q = k× P, де k=1,2,…,n,
де n - порядок підгрупи.

Для базової точки P має місце рівність n∙ P = O.

Приклад. Точка P = (0,1) є базовою для групи точок еліптичної кривої y ² = x ³ + x + 1 (mod 5).

Твердження (теорема Хасе). Значення порядку групи точок еліптичної кривої над полем Галуа GF(q) має верхню і нижню межі:

Приклад. Нехай Q = (2,4) - точка еліптичної кривої

y2 = x3 + x + 1 (mod 5).

Тоді 2∙ Q = (2,1), 3∙ Q = O.

Точка Q = (2,4) породжує циклічну підгрупу порядку 3:
(2,4), (2,1), O.

Визначення. Порядком точки Q еліптичної кривої називається найменше число k, таке що k× Q = O.

Точка Q = (2,4), що належить групі точок еліптичної кривої y ²= x ³ + x + 1 mod 5, має порядок, рівний 3.

4.1.4 Алгоритм обчислення порядку точки еліптичної кривої

Нехай задана еліптична крива y ² = x ³ + ax + b (mod p) над полем GF(p), і точка P належить заданій кривій. Знайдемо порядок точки P. Для цього необхідно вирішити порівняння

x × P = O

(адитивний аналог задачі дискретного логарифмування).

Застосуємо алгоритм великих-малих кроків.

Нехай n - максимальна оцінка порядку групи точок еліптичної кривої, отримана по теоремі Хасе, P - точка еліптичної кривої.

Обчислимо m:= é ù, де é a ù - округлення з надлишком.

1. Будуємо таблицю пар (j, j P) для j = 1, 2, m.
2. Обчисляємо a:= - m P.
3. g:= O.
4. Цикл по i від 0 до m - 1

4.1 перевіряємо, чи є g другою компонентою у таблиці п.1

4.2 якщо g = j P, то вважаємо x = m × i + j

4.3 g:= g + a.

Приклад. Візьмемо еліптичну криву y ² = x ³ + x + 1 над простим полем GF(p), p = 5. По теоремі Хасе максимальна оцінка порядку групи точок кривої дорівнює n = 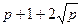= 5+1+2 »10. Звідси m = 4.

За допомогою алгоритму великих-малих кроків знайдемо порядок точки P = (0,1).

Побудуємо таблицю

Знайдемо t:= – m P = – 4 (0,1) = – (3,4) = (3, – 4) = (3,1).

g:= O.

i = 0 g:= g + t = O + (3,1) = (3,1).

i = 1 g = g + t = (3,1) + (3,1) = (0,1).

i = 2 j = 1 Þ x = m × i + j = 4×2 + 1 = 9.

Порядок точки P = (0,1) дорівнює 9.

На рис. 4.3 показаний приклад еліптичної кривої над полем

,

з параметрами a = 1, b = 1, p = 23, 4 a ³+27 b ²=8¹0 (mod 23). Точки кривої визначені як усі рішення рівняння , включаючи нескінченну точку. Отже, порядок групи точок дорівнює 27+1=28.

Рисунок 4.3 - Приклад еліптичної кривої над полем GF(23).

Наведемо протокол цифрового підпису на еліптичних кривих ГОСТ Р 34.10-2001.

Таблиця 4.1 – Протокол цифрового підпису ГОСТ Р 34.10-2001

Формування цифрового підпису	Перевірка цифрового підпису
Вхід: секретний ключ , відкритий ключ , загальносистемні параметри. Вихід: ЦП для повідомлення .	Вхід: відкритий ключ , загальносистемні параметры, ЦП , для повідомлення . Вихід: Підпис дійсний чи ні.
1. ; 2.Обираємо; 3. ; 4. ; 5. .	1. ; 2. ; 3. ; 4. ; 5. ; 6. ; 7.

4.1.5 Алгоритм скалярного множення на еліптичній кривій

Для множення точки еліптичної кривої на велике ціле число застосовується наступний алгоритм:

Вихідні дані: число d ¹0, точка P, еліптична крива E = < a, b, p >.

Результат: точка Q = d ´ P.

1. Якщо d =1, то Q:= P; закінчити роботу алгоритму.

2. k:= l_d –2; Q:= P, де l_d – довжина множника d в бітах;

3. Для i, що приймає значення від k до 0, виконати шаги 4-5.

4. Q:= Q + Q.

5. Якщо i -й біт d дорівнює 1, то Q:= Q+P.

6. Закінчити роботу алгоритму.

Не нашли, что искали? Воспользуйтесь поиском: