
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
СЛАУ, матричный вид СЛАУ
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Лекция 5 Обратная матрица. СЛАУ, матричный вид
Что главное мы узнали на прошлой лекции
На прошлой лекции были определены определители квадратных и изучены их свойства.
Что мы узнаем на этой лекции
Мы перейдем к конкретным приложениям матриц. Одним из важнейшим из них является теория СЛАУ – систем линейных алгебраических уравнений. Обратная матрица, алгоритм ее вычисления
СЛАУ – система линейных алгебраических уравнений. Матричная запись СЛАУ. Метод Крамера, метод Гаусса, матричный метод решения СЛАУ. Вид реальных СЛАУ в прикладной математике.
Обратная матрица
Определение 1. Пусть задана квадратная матрица  . Матрица
. Матрица  называется обратной матрицей к матрице
называется обратной матрицей к матрице  , если выполнено соотношение
, если выполнено соотношение  , где
, где  - единичная матрица той же размерности.
- единичная матрица той же размерности.
Обратную матрицу мы будем обозначать символом  .
.
Теорема 1. Для квадратной матрицы  обратная матрица существует тогда и только тогда, когда определитель матрицы
обратная матрица существует тогда и только тогда, когда определитель матрицы  не равен 0.
не равен 0.
Доказательство. Необходимость. Пусть обратная матрица существует. Так как определитель произведения матриц равен произведению определителей, то справедливо соотношение  . В этом равенстве ни один из множителей не может быть равным 0. Поэтому
. В этом равенстве ни один из множителей не может быть равным 0. Поэтому 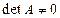 . Необходимость условия теоремы доказана.
. Необходимость условия теоремы доказана.
Достаточность. Пусть определитель матрицы  не равен 0. Докажем, что обратная матрица существует. Доказательство будет носить конструктивный характер. Мы просто в явном виде построим эту матрицу. Одновременно будет показан способ построения обратной матрицы.
не равен 0. Докажем, что обратная матрица существует. Доказательство будет носить конструктивный характер. Мы просто в явном виде построим эту матрицу. Одновременно будет показан способ построения обратной матрицы.
Шаг № 1. Вычислим  и убедимся в том, что он не равен 0.
и убедимся в том, что он не равен 0.
Шаг № 2. Составим матрицу из алгебраических дополнений к элементам матрицы  .
.
Шаг № 3. Транспонируем матрицу, построенную в п. 2.
Шаг № 4. Поделим каждый элемент матрицы, построенной в п. 3, на  .
.
Докажем, что полученная при этом матрица и будет искомой обратной матрицей матрицы  . Пусть заданная матрица имеет вид
. Пусть заданная матрица имеет вид  , тогда после шага 2 мы получим матрицу
, тогда после шага 2 мы получим матрицу  , которая после шага 3 превратится в матрицу
, которая после шага 3 превратится в матрицу  . Найдем произведение этой матрицы и заданной матрицы
. Найдем произведение этой матрицы и заданной матрицы  в том и другом порядке. Итак, запишем
в том и другом порядке. Итак, запишем
 и вычислим все
и вычислим все 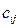 :
:
 ,
,  …
…
Первое из этих равенств справедливо, потому что получается сумма попарных произведений элементов первой строки матрицы  на их алгебраические дополнения, т. е. определитель матрицы
на их алгебраические дополнения, т. е. определитель матрицы  . Второй элемент
. Второй элемент 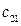 равен 0, т.к. он равен сумме попарных произведений элементов второй строки матрицы
равен 0, т.к. он равен сумме попарных произведений элементов второй строки матрицы  на алгебраические дополнения к элементам ее первой строки, т. е. это разложение по первой строке определителя, у которого первая и вторая строки равны. В итоге все элементы
на алгебраические дополнения к элементам ее первой строки, т. е. это разложение по первой строке определителя, у которого первая и вторая строки равны. В итоге все элементы  , а остальные элементы
, а остальные элементы  , если
, если 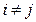 . Аналогичный результат получится при рассмотрении произведения
. Аналогичный результат получится при рассмотрении произведения  , только здесь будет разложения по столбцам матрицы
, только здесь будет разложения по столбцам матрицы  . Теорема доказана, т.к. если в этих произведениях все элементы
. Теорема доказана, т.к. если в этих произведениях все элементы  поделить на
поделить на  , то результатом произведения матриц будет единичная матрица.
, то результатом произведения матриц будет единичная матрица.
Пример 1. Найдем обратную матрицу для матрицы 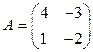 .
.
Шаг № 1. Вычислим 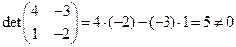 .
.
Шаг № 2. Составим матрицу  из алгебраических дополнений к элементам матрицы
из алгебраических дополнений к элементам матрицы  .
.
Шаг № 3. Транспонируя эту матрицу, получим  .
.
Шаг № 4. Поделим каждый элемент этой матрицы на  и найдем обратную матрицу
и найдем обратную матрицу  .
.
Проверим, что полученная матрица  и будет искомой обратной матрицей. Вычислим
и будет искомой обратной матрицей. Вычислим 
 . Аналогично
. Аналогично  .
.
СЛАУ, матричный вид СЛАУ
В различных приложениях получение важных результатов связано с необходимостью решения СЛАУ – системы линейных алгебраических уравнений. Запишем общий вид СЛАУ
 (1)
(1)
Здесь неизвестные  можно воспринимать как вектор неизвестных
можно воспринимать как вектор неизвестных  , коэффициенты при неизвестных
, коэффициенты при неизвестных  ,
,  ,
,  - как матрицу неизвестных
- как матрицу неизвестных  , правые части
, правые части  можно воспринимать как вектор неизвестных
можно воспринимать как вектор неизвестных 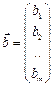 . При таких обозначениях уравнение (1) запишется в виде
. При таких обозначениях уравнение (1) запишется в виде 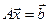 (1’).
(1’).
Пример 2. Запишите систему  в матричном виде и найдите ее решение.
в матричном виде и найдите ее решение.
Запишем систему в матричном виде  . Матрицу
. Матрицу 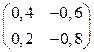 умножим на равные вектора – матрицы размерности
умножим на равные вектора – матрицы размерности  :
:  и
и  . Тем самым мы получим верное равенство
. Тем самым мы получим верное равенство  . В примере 1 мы показали, что матрицы
. В примере 1 мы показали, что матрицы 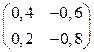 и
и  являются взаимно обратными и их произведение равно единичной матрице
являются взаимно обратными и их произведение равно единичной матрице  . Следовательно,
. Следовательно,  и
и 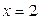 ,
,  .
.
Этот матичный, и другие методы решения СЛАУ мы изучим на следующей лекции.
| <== предыдущая лекция | | | следующая лекция ==> |
| Скандинавская модель по поддержке гендерного равенства | | | Лекция 6 Методы решения СЛАУ |
Не нашли, что искали? Воспользуйтесь поиском: