
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
М. Н. Полякова, А. М. Вербенец 4 страница
Основная цель теоретических основ развития математических представлений — математическое описание и уточнение смысла всего того, что практикуется на занятиях с дошкольниками, разъяснение тех понятий, о которых у детей формируют соответствующие представления. Этой цели и подчинено изложение теоретических основ. Мы не будем строить здесь какие-нибудь строгие математические теории. Все изложение ведется на предматематическом уровне. Для иллюстрации различных понятий, фактов или конструкций мы будем пользоваться примерами и играми, моделирующими эти понятия или конструкции, и соответствующим дидактическим материалом. Таким образом, теоретические основы излагаются в непосредственной связи с элементарными математическими представлениями, формируемыми у дошкольников в процессе их обучения в детском саду. Особенностью этого изложения является выявление логической структуры мышления, развиваемой одновременно с математическими представлениями. Это дает возможность педагогу повысить развивающий эффект при формировании у школьников математических представлений.
Используемая при изложении теоретических основ специальная логическая и математическая терминология и символика не предназначена, разумеется, для обучения дошкольников.
2.1. Множества
Характеристическое свойство множества
Всякое свойство можно рассматривать как принадлежность некоторым предметам.
Например, свойством быть красным обладают некоторые цветы, ягоды, автомашины и другие предметы. Свойством быть круглым обладают луна, мяч, колеса велосипедов и автомашин, детали различных машин и станков и др.
Таким образом, с каждым свойством связывается множество (предметов), обладающих этим свойством. Говорят также, что множество характеризуется данным свойством — или множество задано указанием характеристического свойства.
Под характеристическим свойством множества понимают такое свойство, которым обладают все предметы, принадлежащие этому множеству (элементы этого множества), и не обладает ни один предмет, не принадлежащий ему (не являющийся его элементом).
Иногда свойство отождествляется с множеством предметов, характеризуемым этим свойством. Говоря круглое, мы одновременно мыслим о множестве всех круглых предметов.
Если некоторое множество А задано указанием характеристического свойства Р, то это записывается следующим образом:
А={х\Р(х)}
и читается так: «А — множество всех х таких, что х обладает свойством Р», или, короче, «А — множество всехх, обладающих свойством Р». Когда говорят: «множество всех предметов, обладающих свойством Р», имеются в виду те и только те предметы, которые обладают этим свойством.
Естественно, что некоторым свойством может обладать бесконечное множество предметов, другим — лишь конечное множество. Поэтому множества подразделяются на конечные и бесконечные.
Конечное множество может быть задано непосредственным перечислением всех его элементов в произвольном порядке. Например, множество детей данной группы, живущих на Садовой улице, может быть задано описанием с помощью характеристического свойства:
{х\х — живет на Садовой улице} или же перечислением всех его элементов в произвольном порядке:
{Лена, Саша, Витя, Ира, Коля}.
Вполне понятно, что бесконечное множество нельзя задать перечислением всех его элементов.
Математика в большей мере имеет дело с бесконечными множествами (числа, точки, фигуры и другие объекты), но основные математические идеи и логические структуры могут быть смоделированы на конечных множествах.
Естественно, что в предматематической подготовке обычно имеют дело с конечными множествами.
Элементами таких множеств могут быть самые разнообразные предметы любой природы, как конкретные (растения, животные, предметы обихода и т. д.), так и абстрактные (числа, геометрические фигуры, отношения и т.д.), или изображения таких объектов. Чаще всего мы будем пользоваться множествами, элементами которых являются знакомые детям предметы или их изображения. При этом изображение птички так и будем называть птичкой, изображение дерева — деревом и т. п.
Универсальное множество. Дидактический материал
Обычно предметы, обладающие определенным свойством, выделяются из некоторого наперед заданного основного, или универсального, множества предметов (множества всех предметов, рассматриваемых в связи с данным свойством).
Например, множество детей, живущих на какой-либо улице, мы выделили из множества всех детей определенной (конкретной, известной нам) группы как ее часть (подмножество), характеризуемую указанным свойством. В данном случае множество всех детей этой группы играет роль универсального множества (множества всех детей). Если в качестве универсального множества принять множество всех детей данного детского сада (а не только одной группы), то множество детей, живущих на указанной улице, может оказаться иным.
Все вопросы, связанные с множествами (операции над множествами, отношения между ними, разбиение множества на классы и др.), решаются, как правило, внутри некоторого явно заданного или подразумеваемого универсального множества.
Удобно иллюстрировать понятия, связанные с множествами предметов, на одном универсальном множестве специального дидактического материала, который может быть эффективно использован в обучении дошкольников, — логические блоки'.
Эти блоки названы логическими, потому что они позволяют моделировать разнообразные логические структуры и решать логические задачи с помощью специально создаваемых конкретных ситуаций, т. е. могут быть использованы, как это будет показано дальше, для ранней логической пропедевтики детей 4—6 лет.
Комплект (универсальное множество) состоит из 48 деревянных или пластмассовых блоков. Каждый блок обладает четырьмя свойствами, т. е. является носителем четырех свойств, которыми он полностью определяется: формой, цветом, величиной и толщиной.
Имеются четыре формы: круг, квадрат, треугольник и прямоугольник (под прямоугольником имеется в виду разносторонний прямоугольник; на этом предматематическом уровне дети не считают квадрат
прямоугольником); три цвета: красный, синий,,желтый; две величины: большой и малый — и две толщины: толстый и тонкий. Это так называемый «пространственный вариант» дидактического материала.
Широкие возможности для применения в обучении дошкольников имеет и «плоский вариант» блоков, который для краткости назовем «фигуры». Такой комплект (универсальное множество) состоит из 24 фигур, изображенных на листе плотной бумаги. Каждая из этих фигур полностью определяется тремя свойствами: формой (круг, квадрат, треугольник, прямоугольник); цветом: красный, синий, желтый (к, с, ж); величиной: большой, маленький (б, м). Толщиной фигуры не различаются (она у всех одна и та же). Таким образом, имя каждой фигуры состоит из тройки букв-названий (формы, цвета, величины) и может быть символически записано так: □ жб — квадратная желтая большая фигура (в дальнейшем можно назвать короче — желтый большой квадрат); СИ см — прямоугольная синяя малая фигура (или синий малый прямоугольник) и т. п.
Прежде чем пользоваться блоками (или фигурами) для проведения различных игр и решения разного рода задач, необходимо научиться распознавать каждый элемент универсального множества, состоящего из блоков (или фигур), т. е. уметь называть его полное имя.
Подмножество. Дополнение множества и отрицание предложения
Рассмотрим теперь некоторое свойство, которым могут обладать или не обладать элементы нашего универсального множества.
Свойство быть красным выделяет из универсального множества подмножество красных блоков или фигур. Свойство быть круглым выделяет из этого множества другое подмножество — круглых блоков (или фигур).
Термин подмножество применяется в математике в смысле часть множества. При этом, однако, не исключаются два крайних случая: когда часть множества (подмножество) совпадает со всем множеством, т. е. все элементы множества обладают рассматриваемым свойством, и когда эта часть не содержит ни одного элемента, например ни один блок не обладает свойством быть зеленым. В последнем случае эту часть называют пустым множеством и обозначают символом 0.
Эти крайние случаи тоже можно смоделировать конкретными ситуациями, создаваемыми с помощью блоков (или фигур).
Если, например, рассматривая только красные блоки (теперь множество красных блоков является универсальным), мы предлагаем выделить из них те, которые являются красными, то выделенное подмножество совпадает со всем рассматриваемым множеством. Если же предлагается из этих блоков отделить (переложить в другой ящик) все те, которые являются синими, то этот ящик останется пустым, т. е. фактически в множестве красных блоков будет выделено «пустое множество» блоков.
Пусть множество М — некоторое универсальное множество, множество А — некоторое подмножество множества М. Символически это обозначается «АсМ». Говорят также, что множество А включается в М. Это означает, что все элементы множества А являются также элементами множества М. Выделение подмножества с помощью некоторого свойства может быть смоделировано с помощью игры с одним обручем. Опишем эту игру.
На полу (или на столе) располагают обруч (такой, который используется в художественной гимнастике, или поменьше). У каждого ребенка в руке — один блок. Дети по очереди располагают блоки в соответствии с заданием воспитателя, например внутри обруча — все красные, а вне обруча — все остальные (илл. 4).

Илл. 4
Эта задача, как правило, не вызывает затруднений у детей, уже различающих блоки по цвету и понимающих, что значит внутри и вне обруча. После решения задачи предлагаются два вопроса: «Какие блоки лежат внутри обруча?» и «Какие блоки лежат вне обруча?» Первый вопрос несложен для детей, так как ответ содержится в условии уже решенной задачи. Второй вопрос на первых порах вызывает затруднения, так как в условии задачи говорится «все остальные», здесь же спрашивается «Какие?» Ответ, который мы хотим получить («Вне обруча лежат все не красные блоки»), появляется не сразу. Такой ответ, как «Вне обруча лежат все желтые и все синие блоки», по существу правильный. Но мы хотим выразить свойство блоков, оказавшихся вне обруча, как отрицание свойства тех, которые лежат внутри. Можно предложить детям назвать свойство всех блоков, лежащих вне обруча, с помощью одного слова, используя при этом слово «красные». Некоторые дети догадываются, и в дальнейшем, при проведении этой игры в различных вариантах, эти трудности уже не возникают.
В ходе этой игры отрабатывается переход от выражения некоторого свойства к выражению отрицания этого свойства:
внутри обруча вне обруча
красные не красные
квадратные не квадратные
большие не большие {малые)
толстые не толстые {тонкие)
не круглые круглые
не желтые желтые
и т. п.
Какова же цель применения таких дидактических игр? В дальнейшем будет показано, что такого рода дидактические материалы предшествуют формированию одного из важнейших общеобразовательных умений — умения классифицировать объекты.
Отвлечемся теперь от описанной конкретной игры и рассмотрим илл. 4 как изображение некоторого множества М (с помощью множества точек внутри прямоугольника) и некоторого подмножества А (с помощью множества точек круга), выделенного из М некоторым свойством Р. Оставшиеся элементы М, т. е. те, которые не принадлежат А, не обладают свойством Р. Множество всех этих элементов (тоже подмножество М) называется дополнением множества А (до универсального множества М) и обозначается через 7L {А с чертой). Если множество А характеризуется свойством
Р, то его дополнение А характеризуется свойством не Р (если элементы А красные, то элементы А не красные).
Таким образом, множество А представляет собой множество всех х из М, не обладающих свойством Р. Образование дополнения А приводит к образованию отрицания предложения, выражающего характеристическое свойство множества А.
Отрицание некоторого предложения Р конструируется на русском языке с помощью слов неверно, что, поставленных перед отрицаемым предложением, или, если Р — простое предложение, использованием частицы не перед сказуемым.
Пересечение множеств и конъюнкция предложений
Опишем игру с двумя обручами.
Размещают на плоскости два разноцветных обруча (допустим, красный и черный) так, чтобы они пересеклись (имели общую часть), и предлагают детям расположить блоки так, чтобы внутри красного обруча оказались, например, все красные блоки, а внутри черного — все круглые (илл. 5).
, все красные блоки, а внутри черного — все круглые (илл. 5).
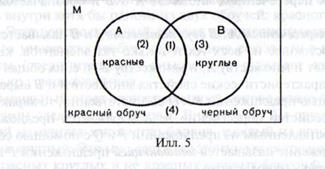
Вначале некоторые дети допускают ошибки. Начиная заполнять красный обруч красными блоками, они могут расположить все эти блоки, в том числе и круглые красные, вне черного обруча. Затем все остальные круглые блоки располагают внутри черного, но вне красного обруча. В результате общая часть двух обручей может оказаться пустой.
Некоторые дети после постановки вопроса «Все круглые блоки внутри черного обруча?» замечают допущенную ошибку и перекладывают круглые красные блоки в общую часть двух обручей, объясняя, почему они должны лежать именно там (внутри красного обруча — потому что красные, внутри черного — потому что круглые).
После выполнения практической задачи по расположению блоков дети отвечают на четыре стандартных для всех вариантов игры с двумя обручами вопроса. Какие блоки лежат: 1) внутри обоих обручей; 2) внутри красного, но вне черного обруча; 3) внутри черного, но вне красного обруча; 4) вне обоих обручей. Следует подчеркнуть, что блоки надо называть здесь с помощью двух свойств — формы и цвета.
Отвлечемся теперь от описанной игры и рассмотрим ситуацию, изображенную на илл. 5, в общем виде1.
Общая часть множеств Д и В (илл. 5, область (1)) представляет собой подмножество всех элементов из М, принадлежащих как А, так и В, т. е. обладающих обоими свойствами Ри Q. Это множество называется пересечением множеств А и В и обозначается через АглВ.
Итак, пересечением Аг\В двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А, и множеству В, т. е. их общая часть.
Если характеристические свойства множеств А и В выражаются с помощью предложений Р и Q соответственно, то характеристическое свойство пересечения АслВ выражается предложением «Ри Q», составленным из предложений PnQc помощью союза и. Это предложение называется конъюнкцией предложений Р и Q (от лат. conjunctio — союз, связь).
| 1 Изображение множеств с помощью кругов было предложено выдающимся математиком Леонардом Эйлером (1707—1783). Поэтому такие круговые диаграммы называют кругами Эйлера, иногда диаграммами Эйлера—Венна. |
Зависимость истинностного значения конъюнкции от истинностных значений составляющих предложений определяется обычным смыслом союза и: конъюнкция «Р и Q» истинна тогда и только тогда, когда истинны оба составляющих ее предложения Р и Q. Это можно записать в виде следующей истинностной таблицы, дающей истинностные значения конъюнкции при любых возможных комбинациях истинностных значений составляющих (см. табл. 1).
| Таблица 1. Истинностные значения конъюнкции | ||||
| Р | Q | PhQ | ||
| И | и | И | ||
| и | д | Л | ||
| гт | И | л | ||
| л | ||||
| л | Л | л |
В логике конъюнкция обозначается знаком «л», т. е. вместо «Р и О» пишут «PaQ».
Объединение множеств и дизъюнкция предложений
Обратимся еще раз к игре с двумя обручами, изображенной на илл. 5. Поставим еще один вопрос: «Какое множество блоков оказалось внутри хотя бы одного из двух обручей: красного или черного?» Этот вопрос сложный, так как характеристическое свойство этого множества требует применения союза или в неразделительном (соединительном) смысле, что вызывает затруднения не только у дошкольников.
Правильный ответ на поставленный вопрос может быть сформулирован следующим образом. Внутри хотя бы одного из двух обручей находится множество блоков, каждый из которых красный или круглый. Это множество состоит из всех красных не круглых, красных круглых и не красных круглых блоков (изображенных соответственно областями (2), (1), (3) в диаграмме (илл. 5).
В общем виде можно сформулировать так. Если множество А характеризуется свойством Р, множество В — свойством Q, то множество, состоящее из всех предметов, являющихся элементами хотя бы одного из этих двух множеств, характеризуется свойством Р или Q.
Это множество называется объединением множеств А и В и обозначается «ЛиВ».
Итак, объединением ЛоВ двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
Союз или понимается здесь в неразделительном смысле, т. е. каждый элемент объединения A\jB должен принадлежать хотя бы одному из множества А, В, т. е. или А, или В, или обоим множествам An В.
Таким образом, если характеристические свойства множеств А и В выражаются с помощью предложений Р и Q соответственно, то характеристическое свойство объединения АиВ выражается предложением «Р или Q», составленным из предложений Р и Q с помощью союза или, понимаемого в неразделительном смысле. Это предложение называется дизъюнкцией предложений Ри Q (от лат. disjunctio — разобщение, различие).
В обыденной речи союз или применяется в двух различных смыслах: неразделительном (соединительном), когда составное предложение, образованное с помощью этого слова, считается истинным в случае, если истинно хотя бы одно из составляющих предложений; в разделительном, когда составное предложение считается истинным в случае, если истинно только одно из составляющих предложений, в этом случае иногда говорят или.., или, либо.., либо.
Разбиение множества на классы
Разбиение множества на классы лежит в основе классифицирующей деятельности.
Обратимся еще раз к диаграмме, изображенной на илл. 4. Здесь мы имеем множество М и два его подмножества Ai~A, удовлетворяющие следующим условиям:
1) каждое из множеств А и ~А непустое, т. е. Аф0 и ~Аф<2>;
2) они не пересекаются, т. е. АпА=0;
3) их объединение образует множество М, т. е. A\JA = М. Условия (1)—(3) определяют разбиение множества М на два
класса (А и Л).
Рассмотрим теперь диаграмму на илл. 5.
Здесь мы имеем множество М и четыре подмножества: АглВ, АпВ, ~Ас\В, ЪглВ. Обозначим их соответственно через К\, К2, A3, А4.
Нетрудно заметить, что выполняются условия, аналогичные предыдущим:
1) каждое из множеств К\, Ki, A3, К4 непусто, т. е. А,*0, где/=1, 2, 3,4;
2) эти множества попарно не пересекаются, т. е. Kf\Kj=<Z, где Щ и i,j = 1, 2, 3, 4;
3) их объединение образует множество М, т. е. AiuA2uA3uA4 = М.
Объединение 'ЩыК^ШрвЩ состоит из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств К\, Ki, A3, А4.
В этом случае условия (1)—(3) определяют разбиение множества М на четыре класса.
Рассмотрим теперь игру с тремя обручами.
Пусть три разноцветных (например, красный, черный и синий) обруча расположены так, как показано на илл. 6.

Илл. 6
После того как образовавшиеся области (1)—(8) соответствующим образом названы (внутри всех трех обручей, внутри красного и черного, но вне синего и т. д.), решается более сложная, чем в игре с двумя обручами, задача классификации блоков (или фигур) по трем свойствам. Предлагается расположить блоки, например, так, чтобы внутри красного обруча оказались все красные блоки, внутри черного — все квадратные, а внутри синего — все большие. После выполнения задачи расположения блоков ставятся восемь стандартных для любого варианта игры с тремя обручами вопросов. Какие блоки лежат: 1) внутри всех трех обручей; 2) внутри красного и черного, но вне синего обруча; 3) внутри черного и синего, но вне красного обруча; 4) внутри красного и синего, но вне черного обруча; 5) внутри красного, но вне черного и вне синего обруча; 6) внутри черного, но вне синего и вне красного обруча; 7) внутри синего, но вне красного и вне черного обруча; 8) вне всех трех обручей?
Как видно на илл. 6, в игре с тремя обручами моделируется разбиение множества на восемь классов:
Ш{ т АпВпС; К2 = АпВиС; Къ = ИглВслС; К4 = АглВпС; К5 = АпВпГ; К6 = InBnC; К7 = InBnC; Ks = InBnC.
И здесь также выполняются условия (1)—(3).
Теперь можно ответить в самом общем виде на вопрос: что такое разбиение множества на классы?
Система множеств К\, К2,... К„ называется разбиением множества М на классы, а сами эти множества — классами разбиения, если выполняются следующие условия:
1) каждое из множеств К\, К2,... К„ непустое, т. е. Kj*0, где / = 1, 2, 3,.., я;
2) эти множества попарно не пересекаются, т. е. Kji~\Kj = 0 для всяких fcj и 1, 2, 3,.., п;
3) их объединение образует множество М, т. е. К{иК2и...К„ = М.
Если хотя бы одно из условий (1)—(3) не выполняется, то система множества К\, К2,.., К„ не является разбиением множества М на классы. Например, система множества остроугольных, прямоугольных и двупрямоугольных треугольников не образует разбиение множества всех треугольников, так как множество двупрямоугольных треугольников, содержащих по два прямых угла, пусто, т.е. не выполняется условие (1). Система множеств остроугольных, прямоугольных и равнобедренных треугольников не образует разбиение множества всех треугольников, так как не выполняется условие (2) — множества прямоугольных и равнобедренных треугольников пересекаются (существуют прямоугольные равнобедренные треугольники). Система множества остроугольных и прямоугольных треугольников не образует разбиения множества треугольников, так как не выполняется условие (3) — объединение множеств остроугольных и прямоугольных треугольников не образует множество всех треугольников.
Отношения между двумя множествами
С целью уточнения вернемся к вопросу об отношении включения одного множества в другое.
Вообще говоря, в математике различаются два вида включения: в широком смысле (нестрогое включение) и в узком смысле (строгое включение). Первое обозначается знаком с. Запись «AczB» означает, что все элементы Л принадлежат В. При этом возможны два случая:
1) все элементы В принадлежат А, т. е. AczB и ВсА. В этом случае множества An В состоят из одних и тех же элементов и называются равными, что обозначается так: «А=В». Например, если А — множество всех больших блоков, а В — множество всех блоков, которые не являются малыми, то А=В. Как видно, равные множества по существу совпадают (при задании их перечислением элементов они могут отличаться лишь порядком перечисления, который несуществен);
2) не все элементы В принадлежат А, т. е. AciB, но BczA. В таком случае говорят также, что А строго включается в В — или А является собственной (или правильной) частью В. Это отношение в математической литературе обычно обозначается символом «с» {A(zB).
В предматематической подготовке дошкольников встречается лишь строгое включение, собственная часть множества.
В играх с обручами моделируются и другие отношения, в которых могут находиться два множества. Так, например, множества красных (А) и не красных (Л) блоков не имеют ни одного общего элемента, т. е. их пересечение пусто (АглА = 0). Такие два множества, как мы уже знаем, называются непересекающимися (в литературе встречается и термин «дизъюнктные» множества). Множества красных (А) и квадратных (В) блоков имеют общие элементы (красные квадраты), т. е. их пересечение непусто (АглВф0), причем ни одно из этих множеств не включается в другое, т. е. не является подмножеством другого. Такие два множества называются пересекающимися.
Выявление правильных отношений между множествами окружающих нас предметов — составная часть формирования и развития представлений дошкольников об окружающем мире. Выработка у дошкольников простейших представлений классификации окружающих предметов является основой для формирования в дальнейшем математического мышления, связанного с моделированием и исследованием различных математических конструкций, способствует повышению алгоритмической культуры учащихся.
2.2. Отношения
Бинарные отношения
Под бинарным отношением понимают отношение между двумя предметами. Дальше, говоря «отношение», мы будем иметь в виду именно бинарное отношение. Выясним, что интуитивно понимают под отношением и как это понятие можно описать математически.
Из курса школьной математики известны многочисленные примеры отношений:
• между числами: равно, не равно, меньше, больше, не меньше, не больше, делит, делится на;
• между точками прямой: предшествует, следует за;
• между прямыми: параллельны, пересекаются, перпендикулярны, скрещиваются;
• между прямой и плоскостью: параллельны, пересекаются, перпендикулярны;
• между плоскостями: параллельны, пересекаются, перпендикулярны;
• между геометрическими фигурами: равно, подобно и др.
Это, разумеется, далеко не полный перечень встречающихся в школьной математике отношений.
Примеры бинарных отношений встречаются не только в математике, но и всюду в жизни, вокруг нас. Родственные и другие отношения между людьми (быть отцом, дедушкой, матерью, бабушкой, братом, сестрой, другом, ровесником; старше, моложе, выше, ниже и др.) выступают как бинарные отношения. Отношения между событиями во времени (раньше, позже, одновременно), между предметами по их расположению в пространстве (выше, ниже, левее, правее, севернее, южнее и др.) также выступают как бинарные отношения.
Всегда, когда речь идет о некотором отношении, имеются в виду два множества А я В; при этом некоторые элементы множества А находятся в данном отношении с некоторыми элементами множества В или того же множества А.
Таким образом, всякое отношение между элементами множеств А и В (или между элементами множества А) порождает множество пар, первые компоненты которых принадлежат А, вторые — В (или тоже А), т. е. порождает подмножество АхВ (или АхА), причем такое, что элементы каждой пары и только они находятся в данном отношении.
Всякое отношение между элементами двух множеств А и В полностью характеризуется тремя множествами: А и В, между элементами которых установлено отношение, и некоторым множеством пар Р — подмножеством АхВ, т. е. декартовым произведением. Один из путей определения математического понятия отношения и состоит в отождествлении этого понятия с указанной тройкой множеств.
Отношением между элементами непустых множеств А и В называется тройка множеств р=(Р, А, В), где P<zAxB.
Множество пар Р называется графиком отношения р.
Об элементах пары (х, у), принадлежащей графику Р, говорят, что они находятся в отношении р, и записывают это так: «хру».
Таким образом, записи «(х, у)е Р» или «хру» равносильны.
Если В—А, то р=(Р, А, А) называется отношением между элементами множества А.
Свойства отношений
1. Отношение р на множестве А является рефлексивным, если всякий элемент этого множества находится в отношении р с самим собой. Если же каждый элемент множества А не находится в этом отношении с самим собой, отношение обладает свойством антирефлексивности и называется антирефлексивным.
Среди уже перечисленных нами отношений рефлексивными являются: равно, не меньше, не больше, делит, делится на, равенство и подобие фигур; антирефлексивными являются отношения: неравно, меньше, больше между числами; предшествует, следует за между точками прямой. Отношение быть ровесником между людьми является рефлексивным, отношение же быть отцом, быть матерью, выше, старше, моложе — антирефлексивными. Отношение быть другом не является ни рефлексивным, ни антирефлексивным (бывают случаи, когда человек сам себе друг, и случаи, когда человек сам себе недруг).
2. Рассмотрим свойство: если а-b, то Ь=а, т. е. если пара (а, Ь)
находится в отношении равно, то и пара (Ь, а) находится в этом
отношении.
Таким свойством обладает, например, отношение быть ровесником: если х ровеснику, то у ровесник х. Это отношение обладает свойством симметричности и называется симметричным.
Не нашли, что искали? Воспользуйтесь поиском: