Тема 4. Показатели вариации.

4.0 Рассчитаем дисперсию и среднее квадратическое отклонение для следующего ряда распределения.

Распределение магазинов города по товарообороту во II квартале.

Группы магазинов по величине товарооборота, тыс. руб.	Число магазинов fi	Середина интервала, тыс. руб. xi
А
40 – 50				-49,2	2420,64	4841,28
50 – 60				-39,2	1536,64	6146,56
60 – 70				-29,2	852,64	5968,48
70 – 80				-19,2	368,64	3686,40
80 – 90				-9,2	84,64	1269,60
90 – 100				0,8	0,64	12,80
100 – 110				10,8	116,64	2566,08
110 – 120				20,64	432,64	4759,04
120 – 130				30,8	948,64	5691,84
130 – 140				40,8	1664,64	4993,92
Итого				-	-	39936,00

Решение. В приведенных ранее примерах мы имели дело с дискретными рядами. при расчете показателей вариации по интервальным рядам распределения необходимо сначала определить середины интервалов, а затем вести дальнейшие расчеты, рассматривая ряд середин интервалов как дискретный ряд распределения.

Результаты вспомогательных расчетов для определения дисперсии и среднего квадратического отклонения содержатся в графах 2 – 6 вышеприведенной таблицы.

Средний размер товарооборота определяется по средней арифметической взвешенной и составляет:

тыс. руб.

Дисперсия товарооборота

.

Среднее квадратическое отклонение товарооборота определяется как корень квадратный из дисперсии:

тыс. руб.

Воспользуемся данными предыдущего примера и рассчитаем дисперсию по способу отсчета от условного нуля и способу моментов. Расчет произведем в табличной форме.

Группы магази-нов по товаро-обороту, тыс. руб.	Число магази-нов fi	Середина интерва-ла, тыс. руб. xi	xi –А (А=95)	(k=10)
40-50			-50	-5	-10
50-60			-40	-4	-16
60-70			-30	-3	-21
70-80			-20	-2	-20
80-90			-10	-1	-15
90-100
100-110
110-120
120-130
130-140
Итого		-	-	-	-8		-

По способу отсчета от условного нуля:

По способу моментов получаем:

По способу разности между средней квадратов вариантов признака и квадратом их средней величины

.

Результаты расчетов дисперсии по всем трем способам дают одну и ту же величину.

5.0. Рассчитать дисперсию по правилу сложения дисперсий.

1 бригада	2 бригада
№ п/п	Изготовлено деталей за 1 час (шт.) (xi)			№ п/п	Изготовлено деталей за 1 час (шт.) (xi)
		-2				-3
		-1				-2
						-1
Итого

Решение. Возьмем средние по каждой группе.

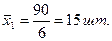
1. Внутригрупповая дисперсия

Средняя из групповых дисперсий.

2. Межгрупповая дисперсия

3. Общая дисперсия или

На основании правила сложения дисперсий можно определить показатель тесноты связи между групповым и результативным признаками, он называется эмпирическим корреляционным отношением.

Отсюда следует, что связь между групповым и результативным признаком существенная.

6.0. Рассчитать дисперсию способом моментов..

Группы фирм по стоимости основных фондов (млн. руб)	Количество фирм (fi)	Середина интервала	k = 0,5
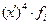
0,5 - 1		0,75	-2	-40		-160
1 – 1,5		1,25	-1	-40		-40
1,5 – 2		1,75
2 – 2,5		2,25
Итого				-60		-180

Определим условные моменты m₁, m₂, m₃, μ ₂, μ ₃.

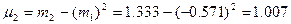
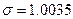
А – условный нуль, в качестве которого используют середину интервала с наибольшей частотой, К – величина интервала.

- незначительная асимметрия.

E_K=0 – симметричное распределение, Е_К>0 – островершинное распределение, Е_К<0 – плосковершинное распределение.

- островершинное распределение.

Не нашли, что искали? Воспользуйтесь поиском: