И качество измерений

Приемочный контроль

Условия выборочного контроля наиболее адекватно отражает гипергеометрический закон распределения, рассмотренный выше. Два других закона используются для упрощенных оценок.

Решение о качестве партии изделий, принимаемой в результате выборочного контроля, требует определения объема выборки п при заданных уровне дефектности q и так называемом браковочном числе А_c..

С позиции теории, такое решение относят к решениям минимизирующим риск, и оно требует нахождения оперативной характеристики, которая определяется следующим образом:

где F(q) — вероятность приемки партии изделий, среди которых доля дефектных изделий составляет q,

А_с — приемочное число (допустимое число дефектных изделий в выборке и);

Р(п, z) — вероятности появления в выборке бракованных изделий, когда z последовательно принимает значения от 0 до А_с.

Иными словами это кумулятивная вероятность и ее можно определить по формуле:

=Р(60,0)+Р(60,1)+Р(60,2)+…Р(60,20),

где n для примера принято равным 60, a z заранее неизвестно и принято в диапазоне 0—20.

Оперативную характеристику можно представить в виде графика F(q)=f(q%), зафиксировав значение n, при заданных значениях А_с и N.

Например, используя гипергеометрический закон распределения при q от нуля до 10, при N = 1200; п = 100 и А_с = 3 получим:

где N= 1200 — объем партии;

N = q ´ N — объем дефектных деталей в партии. Результаты расчетов приведены в табл. 13.1. Полученная опера­тивная характеристика контроля показана на рис 13.1.

Таблица 13.1

Оперативная характеристика плана приемочного контроля

Рис. 13.1. Оперативная характеристика плана приемочного контроля

На рис. 13.1 показаны: a — риск поставщика; b — риск заказчи­ка; AQL — приемочный уровень дефектности (accept— принимать; quality — качество; level — уровень); LQ — браковочный уровень дефектности.

На кривой F(q) = f(q) совпадение заданных AQL и (1 — a) точке М₁ и LQ и b в точке M₂ маловероятно, что и показано на рисунке. Другими словами кривая F(q) =f(q) должна быть согласована с величинами AQL, a, LQ и b.

Покажем процедуру использования оперативной характеристики плана приемочного контроля на численном примере.

Пример. Поставщик (изготовитель) и заказчик (потребитель) договорились, что AQL = 2 %, a = 0,05, LQ = 5 % и b = 0,05. Объем; партии большой, поэтому можно использовать распределение Пу­ассона. Необходимо построить оперативную характеристику и план контроля.

По горизонтальной оси отложим значения AQL и LQ, а по вертикальной оси (1 — a) и b. Оперативная характеристика плана приемочного контроля приведена на рис. 13.2.

При построении графика через точки M₁ и M₂ нужно провести расчетную оперативную характеристику, для чего следует совмест­но решить систему уравнений:

Первое уравнение выражает риск поставщика, второе — риск заказчика.

В системе два уравнения и две неизвестные величины — п и А_с.

Запишем вероятность приема партии F(n;А_с;q= 0,02)=0,95 и вероятность ее браковки F(n; A_c; q = 0,05) = 0,05, используя рас­пределение Пуассона:

Рис. 13.2. Оперативная характеристика плана приемочного контроля на основе распределения Пуассона

Прямого решения этой системы нет, так как она трансцендентна, и ее нужно решать либо с помощью компьютера, либо с помо­щью таблиц функций F(q) =f(q). Учитывая, что

, a=0,05, b=0,05,

и решая систему, получим:

А_с= 12 и =7,69.

Из партии необходимо выбирать изделий.

Если среди 400 изделий окажется менее 12 дефектных, то она принимается, если более 12 дефектных, то она бракуется. При этом 5% партий может ошибочно браковаться и столько же может быть принято по ошибке.

Рассмотрим тенденции изменения вида функции F(q) при изме­нении величин n, А_с:

1. Допустим, что А_с / п = const, но п и А_с увеличиваются (рис. 13.3а). Кривая при этом увеличивает свою крутизну и в преде­ле, когда п = N, выборочный контроль перейдет в сплошной и AQL = LQ.

2. Пусть при n = const, A_c - увеличивается (рис. 13.3б)

3. Если при n=const, А_С увеличивается (Рис. 13.3в), то контроль становится менее жестким.

4. А_С = const; n увеличивается (рис. 13.3г), контроль ужесточается.

Рис. 13.3. Типичные оперативные характеристики планов приемочного контроля

Качество измерений

Напомним, что в соответствии с положениями теоретической метрологии измерение может выполняться с использованием шка­лы порядка (уровней), шкалы интервалов и шкалы отношений.

Во втором и третьем случаях результат измерения является слу­чайной величиной и может записываться выражением:

, или ,

где X — показание средства измерения;

Q — поправка.

Величина Х характеризует правильность показаний, а поправка — точность измерений. По этим параметрам измерительная техника разделяется на классы точности в соответствии с допускаемой по­грешностью измерений.

Приведенная погрешность измеряется в процентах от верхнего предела измерений, относительная погрешность — от результата са­мого показания.

Используется ряд классов точности, в том числе: 0.1, 0.2, 0.5, 1.0, 1.5, 2.5, 4.0. Характеристикой класса является относительная погрешность, указываемая в процентах: 0.1, 0.5, 4.0.

Правильность результата измерения обеспечивается совпадени­ем среднего значения измерений со значением измеряемой величины.

Значение X— величина случайная, поправка 0 не является слу­чайной, она характеризирует относительную погрешность измере­ния.

На рис. 13.4 показано распределение плотности вероятности при точных измерениях (1) и менее точных (2).

Р(х)

Рис. 13.4. Распределение плотности вероятности при двух классах точности измерений

Если значение поправки с течением времени не меняется, то при многократном измерении постоянного размера одним и тем же средством измерений (в одинаковых условиях) получим:

,

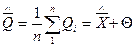где — средний арифметический результат измерений;

n — количество измерений;

— среднее значение показания при измерении;

Q — значение поправки;

Q = const.

Это выражение показывает, что точность многократного измере­ния выше, но правильность такая же, как и при однократном изме­рении.

Пример. При метрологической аттестации вольтметра в нормаль­ных условиях выполнено 100 измерений образцового напряжения в различных точках шкалы. Установлено, что распределение вероят­ности с дисперсией S_u² напряжение равно 1,5В. Смещение средне­арифметического значения в сторону меньших значений с вероят­ностью 0,95 достигает 0,3В. Необходимо сравнить качество одно­кратных и многократных измерений.

Решение примера. Из результатов аттестации следует, что в пока­зания вольтметра нужно вносить поправку Q_U = +0,ЗВ.

Стандартная ошибка (среднеквадратичное отклонение) состав­ляет:

= 1,22В.

Если показания вольтметра U = 20В, то результат измерения можно записать в виде:

U = (20 + 0,3) ±t ´ S_u= 20,3±2,1 ´ 1,22 = 20,3±2,56 В.

Результат измерения: U= 17,74... 22,86 В

Точность многократного измерения выше, и соответствующие показатели качества измерения при девяти отсчетах составят:

Q_U= +0,3 В и = 0,406 В.

Допустим, вольтметр дал девять показаний: 20; 21; 20,5; 21; 20,5; 21,5; 20,5; 20,5; 21,2. Тогда = 20,74.

Результат измерения можно записать следующим образом:

U = (20,74 - 03) ± t ´ 0,406 = 20,04 ± 0852 В,

U= 20,188...21,892.

Погрешность составляет - 4% (D = 0,852 от 21,04).

При одновременном измерении одного и того же размера (пара­метра) разными средствами нужно верно квалифицировать исход­ную информацию.

Допустим, что точность и правильность однократных измерений отдельными средствами измерений неизвестны, но в паспортных данных приборов приводится значение поправки, которую нужно внести в показание. Результат измерения Q = X+ Q можно рассмат­ривать как сумму двух случайных величин:

,

где m — число измерений.

Если X и Q подчиняются нормальному закону распределения, то точность и правильность определяют с использованием формул:

,

В рассматриваемом случае поправка (рассматривается как слу­чайная величина). Такая процедура называется рандомизацией. При­веденные формулы показывают, что рандомизация результата из­мерения одного и того же параметра улучшается и по точности и по правильности.

Пример. В табл. 13.2 приведены числовые значения X_i одиннадца­ти измерений одного и того же параметра разными средствами из­мерений. Даны поправки Q_i, заимствованные из паспортных данных. Вычислим средние значения измеренного параметра и поправок приборов:

,

После этого определим, в каких пределах находится измеряемое значение и каковы показатели качества результата измерения.

Таблица 13.2

Не нашли, что искали? Воспользуйтесь поиском: