
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ИЗМЕРЕНИЕ и КОДИРОВАНИЕ ИНФОРМАЦИИ
I. Единицы измерения информации
За единицу количества информации принят 1 бит – количество информации, содержащееся в сообщении, уменьшающем неопределенность знаний в 2 раза.
Принята следующая система единиц измерения количества информации:
1 байт – 8 бит (23 бит)
1 Килобайт – 210=1024 байт (213 бит)
1 Мегабайт – 210=1024 Килобайт (223 бит)
1 Гигабайт – 210=1024 Мегабайт (233 бит)
1 Терабайт – 210=1024 Гигабайт (243 бит)
Задача № 1.
Заполните таблицу:
| Кол-во бит | Кол-во байт | Кол-во Кбайт | Кол-во Мбайт | Кол-во Тбайт |
| ? | ? | ? | ? |
Решение: для получения искомой величины в байтах поделим количество бит на 8, далее получаемые величины делим каждый раз на 1024.
| Кол-во бит | Кол-во байт | Кол-во Кбайт | Кол-во Мбайт | Кол-во Тбайт |
| 0,5 |
***
II. Количество информации как мера уменьшения неопределенности
Если некоторое сообщение, получаемое потребителем, приводит к уменьшению неопределенности его знаний, то это означает, что такое сообщение содержит информацию.
Задача № 2.
В закрытом ящике лежат 2 шара - черный и белый. Вытаскиваем 1 шар. Какое количество информации будет содержать сообщение о цвете вынутого шара?
Решение: перед вытаскиванием шара существовала неопределенность знания, так как возможны 2 события: «вытащен черный шар» или «вытащен белый шар». После того как шар вытащен, наступает полная определенность: если имело место событие «вытащен черный шар», тогда в ящике остался белый; и наоборот. Вытаскивание одного из двух шаров приводит к уменьшению неопределенности знания в 2 раза.
Рассмотрим понятие “вероятность”. Если N – общее число возможных исходов какого-то процесса (например, вытаскивания шаров), которые могут произойти k раз, то вероятность этого события Р можно определить по формуле: P=k/N.
Вероятность выражается в долях единицы. Для задачи № 2 вероятность вытаскивания как белого, так и черного шара равна 1/2, т.е. события (вытаскивания шаров) равновероятны. Вероятность достоверного события равна 1 (например, из 10 белых шаров вытащен белый шар) и такое событие неинформативно, т.е. количество информации в нем равно 0; вероятность недостоверного (невозможного) события равна 0 (например, из 10 белых шаров вытащен черный шар).
Американский инженер Р.Хартли в 1928 г. рассматривал процесс получения информации как выбор одного сообщения из конечного наперед заданного множества N равновероятных сообщений, а количество информации I, содержащейся в выбранном сообщении, определял как двоичный логарифм N.
Пусть Х – количество информации в сообщении о том, что вытащен белый шар. Тогда 2*х=1/0,5 ® 2*х=2 ® х=1 бит, или по формуле Р.Хартли: I=log2N=log22=1 бит, т.е. доказано, что сообщение об одном событии из двух равновероятных содержит 1 бит информации.
***
Задача № 3.
Нужно угадать одно число из набора чисел от 1 до 100.
Решение: по формуле Р.Хартли можно вычислить, какое количество информации для этого требуется: I=log2100≈6,64. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,64 бит.
***
Задача № 4.
В закрытом ящике лежат 4 шара – 3 черных и 1 белый. Какое количество информации будет содержать сообщение о цвете вынутого шара?
Решение: вытаскиваем 1 шар. Его цвет, скорее всего, будет черным, но может быть и белым. Определим вероятность вытаскивания белого и черного шаров:
N=4; Рбел=1/4=0,25; Рчерн=3/4=0,75.
Информация в каком сообщении о цвете вынутого шара ценнее: «вытащен черный шар» или «вытащен белый шар»? Конечно, информация о том, что вытащили белый шар ценнее, т.к. с этим сообщением получено полное знание – в ящике остались только черные шары.
Информация о том, что вытащили черный шар, тоже уменьшает неопределенность знания (после этого события в ящике осталось 3 шара – 1 белый и 2 черных), но такое сообщение не дает полного знания, например, какой шар может быть вытащен следующим. Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить следующим образом: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии. Рбел ≠ Рчерн и Рбел < Рчерн
Для задач такого рода американский ученый К.Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность выделения сообщений в наборе.
Формула К.Шеннона: I= –(Р1log2Р1+Р2log2Р2+…+РNlog2PN), где i=(1, …, N) и Pi – вероятность того, что именно i–е сообщение выделено в наборе из N сообщений. Каждое слагаемое формулы К.Шеннона выражает кол–во информации, содержащееся в сообщении о том, что произошло определенное событие из имеющегося набора.
Определим кол–во информации в сообщении «вытащен черный шар»:
I= –3/4* log23/4≈0,3 бита.
Определим кол–во информации в сообщении «вытащен белый шар»:
I= –1/4* log21/4=0,5 бита.
Определим общее кол–во информации:
I= –(1/4* log21/4+3/4* log23/4)≈0,8 бита.
***
Заметим, что если вероятности Р1,…,РN равны, то каждая из них равна 1/N и формула К.Шеннона превращается в формулу Р.Хартли.
Задача № 5.
В мешке лежат 64 монеты. Сообщение о том, что достали золотую монету, несет 4 бита информации. Сколько золотых монет было в мешке?
Решение: известно: N=64; Iзол=4 бита; kзол=1; найти nзол –?
Поскольку сообщение о том, что достали золотую монету, несет 4 бита информации, то по формуле Р.Хартли (см. задачу № 2) можно записать:
nзол=kзол/рзол=1/рзол; 24=1/рзол ; отсюда можно найти вероятность вытаскивания золотой монеты: рзол=1/16.
С другой стороны, рзол=nзол/N, следовательно, nзол=N*рзол=64 * 1/16=4. Ответ: число золотых монет в мешке – 4 шт.
***
Задача № 6.
Решить уравнение: 8Х (бит)= 32 (Кбайт)
Решение: выровняем размерности в обоих частях уравнения с учетом: 1 Кбайт=213 бит. Приведем обе части уравнения к основанию 2 и получим: 23*Х=25*213 или 23*Х=218; получим уравнение 3*Х=18, х=6.
***
Задача № 7.
Из двух одинаковых наборов карандашей по 6 цветов в каждом вынимают 2 карандаша, по 1 из каждого набора. Какое количество информации будет содержать сообщение о цвете вынутого карандаша?
Решение: возможное кол-во комбинаций определяется по формуле:
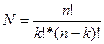 , где n – кол-во элементов в наборе, k – кол-во элементов в выборке.
, где n – кол-во элементов в наборе, k – кол-во элементов в выборке.
n=12, k=2, N=12!/(2!*(12-2)!)=66, I=log266≈6,04 бита.
***
Задача № 8.
Какое минимальное количество вопросов достаточно задать, чтоб определить однозначно месяц рождения опрашиваемого?
Решение: будем считать, что 12 месяцев – это 12 возможных событий; правильно будет задавать «двоичные» вопросы, уменьшающие неопределенность в 2 раза и на которые можно отвечать «да/нет». По формуле Р.Хартли: I=log212≈3,6 бита. Последовательность вопросов:
1. Какое полугодие?
2. Какой квартал из названного полугодия?
3. Какой месяц? (1-й из названного квартала)
4. Какой месяц? (2-й из названного квартала)
***
III. Определение количества информации,
представленной с помощью знаковых систем
Если рассматривать символы алфавита как набор N событий, то кол-во информации несомое одним символом определяется по формуле К.Шеннона, а если появление каждого символа равновероятно – то по формуле Р.Хартли или из уравнения: N=2I. Кол-во информации несомое одним символом тем больше, чем больше знаков в составе алфавита, т.е. чем выше мощность алфавита. Кол-во информации, содержащейся в сообщении, закодированном с помощью знаковой системы, равно кол-ву информации, которое несет 1 знак, умноженному на число знаков в сообщении.
Задача № 9.
Какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1,25 Кбайта?
Решение: переведем информационный объем сообщения биты:
I=1,25*1024*8=10240 бит; определим кол-во бит, приходящееся на 1 символ: 10240/2048=5 бит; определим по уравнению (см. выше) кол-во символов в алфавите: N=2I=25= 32 символа.
***
Задача № 10.
Книга содержит 100 страниц, на каждой из которых 35 строк по 50 символов в каждой. Определите объем информации в книге, если известно, что 1 символ занимает 1 байт. Ответ дайте в Мбайтах.
Решение: 100*35*50*1=175000 байт в книге;
175000/1024≈170,89 Кбайт; 170,89/1024≈0,17 Мбайт.
***
Задача № 11.
Предположим, что 1 символ занимает 1 байт. Какое кол-во различных символов закодировано в сообщении? Сообщение:
Решение: разделим последовательность символов сообщения на группы по 8 символов, т.е. на байты:
10101010 10110111 10110111 01010101 10101010
a b c d e
Очевидно, что группы а и е совпадают, также совпадают группы b и с, следовательно, в сообщении закодировано 3 различных символа.
***
IV. Кодирование графической информации
Аналоговые графические изображения при преобразовании в цифровой компьютерный формат дискретизуются в растровое изображение, каждая точка которого может иметь свой цвет. Качество растрового изображения определяется:
· разрешением – кол-вом точек по вертикали и горизонтали (800*600, 1024*768, 1152*864, 1280*720, 1280*768, 1280*800, 1280*960, 1280*1024);
· палитрой цветов – 16, 256, 65536 цветов;
· глубиной цвета – кол-во бит для хранения цвета точки;
Задача № 12.
Определите объем видеопамяти ПК, необходимый для реализации графического режима монитора с разрешающей способностью 1024*768 точек и палитрой из 65536 цветов. Ответ дайте в Мбайтах.
Решение: определим глубину цвета: I=log265536=16 бит;
определим кол-во точек в изображении: 1024*768=786432;
необходимый объем памяти равен: 16*786432=12582912 бит ≈1,2 Мбайт.
***
Задача № 13.
Определите максимально возможную разрешающую способность для монитора с диагональю 15” и размером точки экрана 0,28 мм.
Решение: выразим размер диагонали монитора в сантиметрах
(1 дюйм ≈ 2,54 см): 2,54*15=38,1 см длина диагонали;
Определим соотношение между высотой и шириной экрана для режима 1024*768 точек: 768/1024=0,75;
предположим, что ширина экрана Х см, тогда высота экрана 0,75*Х см;
по теореме Пифагора найдем ширину:
Х2+(0,75*Х)2=38,12 ® ширина экрана 30,5 см;
кол-во точек по ширине: 305 мм/0,28 мм=1089, следовательно максимально возможное разрешение 1024*768.
***
Задача № 14.
Предположим, что сканируется цветное изображение размером 10*10 см. Разрешающая способность сканера 600 dpi (dot per inch – точки на дюйм). Глубина цвета 32 бита. Какого объема получится графический файл?
Решение: определим разрешающую способность сканера в точках на сантиметр: 600/2,54≈236 точек/см;
кол-во точек в изображении: 10*236*10*236=5569600;
объем файла: 32*5569600=178227200 бит≈21 Мбайт.
***
V. Кодирование звуковой информации
Задача № 15.
Определите объем стереоаудиофайла длительностью звучания 1 минута, если «глубина» кодирования 16 бит, а частота дискретизации 48 кГц.
Решение: объем звукового файла длительностью 1 секунда:
16 бит * 48000 Гц * 2 = 1536000 бит = 187,5 Кбайт;
объем звукового файла длительностью 1 минута:
187,5 Кбайт * 60 сек ≈ 11 Мбайт.
***
| <== предыдущая лекция | | | следующая лекция ==> |
| Теоретическая часть. | | | Содержательный подход. |
Не нашли, что искали? Воспользуйтесь поиском: