Безразмерные критерии подобия

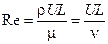− число Рейнольдса (ρ − плотность, U − скорость, L − длина, μ − динамическая вязкость жидкости, ν − кинематическая вязкость жидкости);

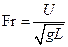− число Фруда (g − ускорение свободного падения);

− число Маха (a − скорость звука);

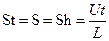− число Струхаля (t − время);

− число Прандтля (c_p − теплоемкость, λ − теплопроводность);

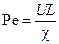− число Пекле (χ − коэффициент температуропроводности);

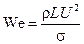− число Вебера (σ − коэффициент поверхностного натяжения).

Задачи

14.25. Что займет больше времени: прожарить одну сковороду толстых котлет или последовательно две сковороды в два рапа более тонких котлет? Полагать, что уложенные на сковороде котлеты можно схематизировать в виде бесконечного слоя, на нижней границе которого задается температура печки T ₁, а верхняя граница теплоизолирована. За время прожаривания принять время, за которое температура на верхней границе до­стигнет величины Т ₂. Начальная температура слоя равна T ₀.

Указание. Процесс нагревания слоя описывается уравнением , где − коэффициент температуропроводности (вывод этого уравнения можно посмотреть здесь). Следовательно, время t ₁ достижения температуры Т ₂ на верхней границе зависит только от толщины слоя h, а также от 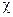, T ₁, Т ₀, T ₂: t ₁ = t ₁(h, 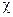, T ₁, Т ₀, T ₂). Применение П-теоремы показывает, что t ₁ = h²f (T ₁/ T ₀, T ₂/ T ₀)/χ. Таким образом, при одинаковых 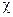, T ₁, Т ₀, T ₂ время t ₁ пропорционально h ². Поэтому прожарить одну сковороду толстых котлет требует в два раза больше времени, чем последовательно прожарить две сковороды в два раза более тонких котлет.

9.191*. Скорость истечения воды из сосуда через малое отверстие определяется формулой 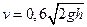, где h − высота уровня воды над отверстием, g − ускорение свободного падения (принять g = 10 м/с²). За какое время вытечет вся вода из цилиндрического бака с диаметром 2 R = 1 м и высотой H = 1,5 м через отверстие в дне диаметрам 2 r = 0,05 м?

1. Найти связь между числами Рейнольдса, Пекле и Прандтля.

2. Дано уравнение

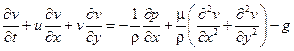
Известно, что процесс, описываемый этим уравнением, происходит в плоской области характерной длины 10 м и ширины 1 м за 5 с; скорость u меняется от 0 до 10 м / с; v − от 0 до 0,1 м / с; ρ = 1 кг / м ³; μ = 10⁻⁵ Па∙с. Характерный перепад давления p − 10⁵ Па; g − ускорение свободного падения вблизи поверхности Земли. Записать данное уравнение в безразмерной форме (если можно пренебречь малыми слагаемыми). Посчитать число Рейнольдса.

88. Парашютист прыгнул с высоты 1.5 км, а раскрыл парашют на высоте 0.5 км. Сколько времени он падал до раскрытия парашюта? Известно, что предельная скорость падения человека в воздухе нормальной плотности составляет 50 м/сек. Изменением плотности с высотой пренебречь. Сопротивление воздуха пропорционально квадрату скорости.

Ответ: Скорость 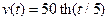, путь 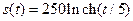; 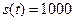при , .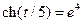

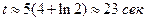В связи с задачей 88 обсудить:

1. Модель, описывающую вертикальное падение тяжелого тела с высоты Н в сопротивляющейся среде.

2. Безразмерный параметр решения задачи из п.1.

3. Построение решения в зависимости от безразмерного параметра.

4. Предельная скорость при сопротивлении, пропорциональ­ном квадрату скорости.

5. Время выхода на предельную скорость.

6. Время падения тела на землю в единицах времени свободного падения в зависимости от безразмерного параметра.

7. Затяжной прыжок парашютиста. Безопасное время падения без парашюта. Своевременное раскрытие парашюта.

Домашнее задание

3. Дано уравнение

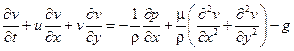
Известно, что процесс, описываемый этим уравнением, происходит в плоской области характерной длины 100 м и ширины 1 м за 5 ч; скорость u меняется от 0 до 10 м / с; v − от 0 до 0,1 м / с; ρ = 1000 кг / м ³; μ = 10⁻³ Па∙с. Характерный перепад давления p − 10⁵ Па; g − ускорение свободного падения вблизи поверхности Земли. Записать данное уравнение в безразмерной форме (если можно пренебречь малыми слагаемыми). Посчитать число Фруда.

89. Футбольный мяч весом 0,4 кГ брошен вверх со скоростью 20 м/сек. Сопротивление воздуха пропорционально квадрату скорости и равно 0,48 Г при скорости 1 м/сек. Вычислить время подъема мяча и наибольшую высоту подъема. Как изменятся эти результаты, если пренебречь сопротивлением воздуха?

Не нашли, что искали? Воспользуйтесь поиском: