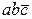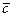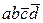Мінімізація за допомогою карт Вейча

Карта Вейча – це прямокутна або квадратна таблиця, число клітин в якій дорівнює – по кількості мінтермів (конституент одиниці) для логічної функції від n -змінних. Кожній клітині приписується номер певного набору значень аргументів (конституент одиниці). У самих клітинах записуються значення функції, визначені на цих наборах. Слід відмітити, що карти Вейча для n змінних можуть мати різний вигляд: як квадрати, так і прямокутники, прямокутники можна видовжити горизонтально або вертикально, клітини карти можна позначати номерами наборів різними способами. На рис. 3.2 – 3.4 подано карти Вейча для двох, трьох і чотирьох змінних, одержаних за допомогою наступних правил.

Карта для двох змінних (рис. 3.2 складається з =4 клітин, для трьох змінних (рис.3.3) – із клітин і т. д. Таким чином, карта для n змінних містить у два рази більше клітин, ніж карта для (n -1)-ї змінної. При цьому подвоєння кількості клітин здійснюється у відповідністю з діаграмою:

2®3 ­ 4 ®5 ­ 6®7 ­ 8®9 ®...,

де цифри позначають кількість змінних, а стрілки – напрямок подвоєння карти. Зокрема, для одержання карти функції від трьох змінних карту функції від двох змінних подвоюємо горизонтально, при переході до карти функції від чотирьох змінних, карту функції від трьох змінних подвоюємо вертикально і т. д.

Означення. Дві однакового рангу кон’юнкції і , які є логічними добутками одних і тих самих змінних, називаються сусідніми, якщо яка-небудь змінна входить в одну з кон’юнкцій із запереченням, а в другу – без нього.

Склеювати можна лише сусідні кон’юнкції, тобто кон’юнкції, які знаходяться в сусідніх клітинах. В результаті склеювання змінна, яка входить в одну з кон’юнкцій із запереченням, а в другу – без нього, випадає, наприклад,

.

Розглянемо один з можливих способів нумерації клітин номерами наборів (конституент одиниці).

Клітину в правому нижньому кутку карти для будь-якої кількості змінних позначимо номером 0.

В картах Вейча для n £ 4 змінних, номери усіх конституент одиниці, сусідніх даній, розташовані в геометрично сусідніх клітках. Серед конституент одиниці для n змінних кожна конституента має n сусід­ніх. В карті для двох змінних, наприклад, для конституенти 0 сусідніми є конституенти 1 і 2. Оскільки номером 0 позначена клітина в нижньому правому кутку, то геометрично сусідню зверху позначимо через 1, а зліва – через 2 або навпаки. Клітину, яка залишилася вільною, позначимо через 3. В клітинах лівого і правого крайніх стовпців карти для трьох змінних ставимо подвоєні номери лівого і правого стовпців карти для двох змінних, а в геометрично їм сусідні клітини – номери, більші на оди­ницю. В клітини верхнього і нижнього крайніх рядків карти для чотирьох змінних ставимо подвоєні номери відповідно верхнього і нижнього рядків карти для трьох змінних, а в геометрично їм сусідні клітини – номери, більші на одиницю.

Зауваження. У літературі можна зустріти і іншу нумерації клітин карт Квайна.

На рис. 3.2 – 3.4 показано приклади умовного розташування змінних на мінімізуючих картах, десяткові номери клітин та відповідні їм мінтерми.

Рис. 3.2

Рис. 3.3

Рис. 3. 4

Алгоритм мінімізації за допомогою карт Вейча зводиться до наступного:

1. На карті Вейча для логічної функції від n змінних виділяють прямокутні області, які об’єднують вибрані одиничні значення функції (лог. 1). Кожна область повинна містити клітинок. Вибрані області можуть перетинатися, тобто одна або декілька клітинок можуть належати різним областям.

2. Кожній із виділених областей, яка складається із клітинок, відповідає мінтермів, які можна склеїти за k змінними, в результаті чого дістаємо елементарну кон’юнкцію рангу , яку часто називають імплікантою.

3. Із виділеної множини областей, вибирають мінімальну кількість максимально великих областей (по кількості клітин), які охоплюють усі клітини з одиничними значеннями логічної функції.

4. Логічно сумують імпліканти, які відповідають вибраним областям. Одержана сума утворює мінімальну диз’юнктивну нормальну форму (МДНФ), тобто є мінімальним покриттям логічної функції за індексом простоти (покриття Квайна).

Зауважимо, що при об’єднанні клітин з одиничними значеннями логічної функції одержують МДНФ самої функції, а при об’єднанні клітин з нульовими значеннями функції – МКНФ, функції інверсної до заданої. Це легко пояснити за допомогою однієї з аксіом булевої алгебри, згідно з якою . Застосувавши до одержаної інверсної мінімальної форми закон де Моргана і , одержимо мінімальну функцію, записану у вигляді ДНФ.

Приклад 3.8. Користуючись картами Вейча мінімізувати нижче наведені функції:

(рис. 3.5, а);

(рис. 3.5, б);

(рис. 3.5, в).

Рис. 3.5

Розв’язання. На кожній із карт виділимо прямокутні області макси­мальної площі і виконаємо склеювання відповідних мінтермів.

У випадку а) маємо логічну суму двох мінтермів, яка склеюється за змінною b: . Отже, .

У випадку б) маємо дві прямокутні області по дві клітини, яким відповідають логічні суми по два мінтерми і один прямокутник, який складається з однієї клітини, якій відповідає один мінтерм:

, , .

Виконавши операції склеювання та логічне сумування, одержаних імплікант, дістанемо .

У випадку в) маємо один прямокутник, який складається з чотирьох клітин, який охоплює чотири крайні мінтерми і дві прямокутні області по дві клітини, яким відповідають логічні суми по два мінтерми:

, , .

Виконавши операції склеювання та логічне сумування, одержаних імплікант, дістанемо .

Приклад 3.9. Користуючись картою Вейча мінімізувати функцію

.

Рис. 3.6

У даному випадку усі одиничні клітини можна охопити двома прямокутниками (2–3–6–7 та 1–3), яким відповідають логічні суми:

, .

МДНФ має вигляд .

Цей самий результат можна дістати, якщо розглядати покриття нульових значень функції. У цьому випадку оптимальне покриття можна здійснити за допомогою двох прямокутників: 4–5 і 4–0. Виділеним прямокутникам відповідають логічні суми: , . Мінімальна функція має вигляд .

Можна показати, що одержані мінімальні функції еквівалентні. Справді, скориставшись законом де Моргана, знайдемо

.

Якщо до одержаного виразу застосувати розподільний закон, то одержимо

.

Що і треба було показати.

Не нашли, что искали? Воспользуйтесь поиском: