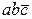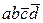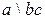Мінімізація за допомогою карт Карно

Карта Карнотак само, як і карта Вейча – це прямокутна або квадратна таблиця, число клітин в якій дорівнює – по кількості мінтермів (конституент одиниці) для логічної функції від n -змінних. В карті Карно, на відміну від карти Вейча, робиться розмітка рядків і стовпців змінними, що відповідає коду Грея. На рис. 3.7 наведено вигляд карт і розмітки рядків і стовпців за кодом Грея для двох, трьох, чотирьох і п’ятьох змінних.

Рис. 3.7

Як і в картах Вейча, кожній клітині приписується номер певного набору значень аргументів. На рис. 3.8 – 3.10 подано карти Карно для двох, трьох і чотирьох змінних, де показано приклади розмітки рядків і стовпців, десяткові й двійкові номери клітин та відповідні їм мінтерми.

Зауважимо, що десяткові і двійкові номери відповідних клітин в картах Дейча і Карно змінюються в залежності від кількості змінних, що спричиняє певні незручності.

Рис. 3.8

Рис. 3.9

Рис. 3. 10

Алгоритм мінімізації за допомогою карт Карно зводиться до наступного:

1. Зображають карту Карно для n змінних і роблять розмітку її рядків і стовпців. У клітини таблиці, які відповідають мінтермам (одиничним наборам) функції, що мінімізується, записують одиницю.

2. На побудованій карті для функції від n змінних виділяють максимальні прямокутні або квадратні області, які об’єднують вибрані одиничні значення функції. Кожна область повинна містити клітинок. Вибрані області можуть перетинатися, тобто одна або декілька клітинок можуть належати різним областям. Чим менше прямокутників і чим більше клітин у прямокутниках, тим краще покриття. З декількох варіантів вибирають той, у якого менший коефіцієнт покриття , де 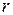– загальне число прямокутників, – їхня сумарна площа в клітинках. Наприклад, для зображеного покриття (рис. 3.19 г) маємо .

4. Формули, отримані в результаті мінімізації, містять 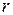елементарних кон’юнкцій (за числом прямокутників в покритті). Кожна кон’юнкція містить тільки ті змінні, які не змінюють свого значення в наборах, що склеюються у відповідному прямокутнику. Число змінних у кон’юнкції називається її рангом. При склеюванні двох сусідніх клітинок одержують ранг кон’юнкції , чотирьох – 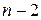, восьми – і т.д.

Приклад 3.10. Користуючись картами Карно мінімізувати нижче наведені функції:

(рис. 3.11, а);

(рис. 3.11, б);

(рис. 3.11, в).

Рис. 3.11

Розв’язання. На кожній із карт виділимо прямокутні області макси­мальної площі і виконаємо склеювання відповідних мінтермів.

У випадку а) маємо логічну суму двох мінтермів, яка склеюється за змінною b: . Отже, .

У випадку б) маємо дві прямокутні області по дві клітини, яким відповідають логічні суми по два мінтерми і один прямокутник, який складається з однієї клітини, якій відповідає один мінтерм:

, , .

Виконавши операції склеювання та логічне сумування, одержаних імплікант, дістанемо .

У випадку в) маємо один прямокутник, який складається з чотирьох клітин, який охоплює чотири крайні мінтерми і дві прямокутні області по дві клітини, яким відповідають логічні суми по два мінтерми:

, , .

Виконавши операції склеювання та логічне сумування, одержаних імплікант, дістанемо .

Приклад 3.11. Користуючись картою Карно мінімізувати функцію

.

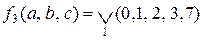Рис. 3.12

У даному випадку усі одиничні клітини можна охопити двома прямокутниками (0–1–3–2 та 3–7), яким відповідають логічні суми:

, .

МДНФ має вигляд .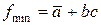

Цей самий результат можна дістати, якщо розглядати покриття нульових значень функції. У цьому випадку оптимальне покриття можна здійснити за допомогою двох прямокутників: 4–5 і 4–6. Виділеним прямокутникам відповідають логічні суми: , . Мінімальна функція має вигляд .

Можна показати, що одержані мінімальні функції еквівалентні. Справді, скориставшись законом де Моргана, знайдемо

.

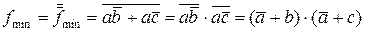Якщо до одержаного виразу застосувати розподільний закон (випадок б), то одержимо

.

Що і треба було показати.

Не нашли, что искали? Воспользуйтесь поиском: