
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод непосредственного интегрирования
Лекция 16 Основные методы интегрирования (2ч)
Содержание лекции: Основные методы интегрирования: непосредственное интегрирование; замена переменной (метод подстановки); интегрирование по частям.
Проинтегрировать функцию – значит, найти хотя бы одну ее первообразную. Рассмотрим основные методы интегрирования, которые позволяют преобразовывать данный интеграл и цель этих преобразований – привести данную задачу интегрирования, сразу или через несколько шагов, к одной или нескольким табличным формулам. Существует несколько методов интегрирования:
I. непосредственное интегрирование;
II. замена переменных;
III.интегрирование по частям.
Рассмотрим каждый из них.
Метод непосредственного интегрирования
Под непосредственным интегрированием будем понимать приведение заданного интеграла к одному или нескольким табличным с помощью тождественных преобразований подынтегрального выражения и свойств неопределенного интеграла. Рассмотренные в предыдущей лекции примеры демонстрировали применение тождественных преобразований и свойства линейности для приведения заданного интеграла к нескольким табличным.
Рассмотрим особо применение свойства 6 к вычислению неопределенного интеграла:
если 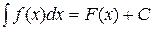 , то
, то 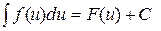 для любой дифференцируемой функции и = и (х).
для любой дифференцируемой функции и = и (х).
Это свойство позволяет значительно расширить таблицу простейших интегралов, так как в силу его все формулы таблицы справедливы не только для независимой переменной х, но и в случае, когда х – дифференцируемая функция какой-либо другой переменной.
Например, 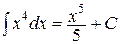 , но и
, но и 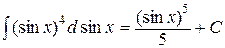 , и
, и 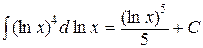 .
.
Или 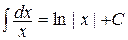 и
и  ,
, 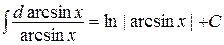 .
.
В рассмотренных интегралах 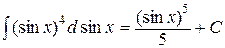 ,
, 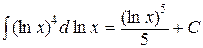 ,
, 
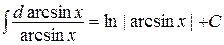 подынтегральная функция есть сложная функция некоторой переменной
подынтегральная функция есть сложная функция некоторой переменной 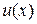
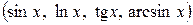 , и под знаком дифференциала стоит эта же функция
, и под знаком дифференциала стоит эта же функция 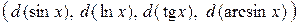 . При этом каждый из интегралов, на основании свойства 6, является табличным. В некоторых случаях в заданном подынтегральном выражении удается сформировать дифференциал некоторой функции
. При этом каждый из интегралов, на основании свойства 6, является табличным. В некоторых случаях в заданном подынтегральном выражении удается сформировать дифференциал некоторой функции 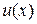 так, чтобы этот дифференциал в совокупности с остальным выражением составляли табличную формула относительно функции
так, чтобы этот дифференциал в совокупности с остальным выражением составляли табличную формула относительно функции 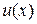 . Такой прием называется подведением под знак дифференциала. При этом используется тот факт, что
. Такой прием называется подведением под знак дифференциала. При этом используется тот факт, что 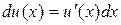
Рассмотрим примеры.
Пример2.
а)  ;
;
б) 
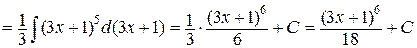 .
.
в) 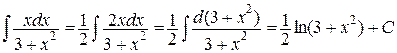
(в последнем примере записано ln(3 + x 2) вместо ln|3 + x 2|, так как выражение 3 + x 2 всегда положительно).
Выведем несколько дополнительных формул, которые наряду с табличными желательно запомнить.
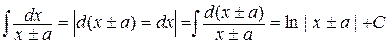
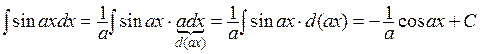 ,
,
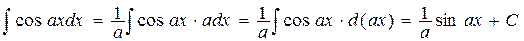 ,
,
Не нашли, что искали? Воспользуйтесь поиском: