Линейные системы дифференциальных уравнений – общая теория

Лекция 28. Системы обыкновенных дифференциальных уравнений

Содержание лекции:

Нормальная система дифференциальных уравнений, ее решение. Задача Коши. Теорема существования и единственности решения. Геометрическая и физическая интерпретация системы дифференциальных уравнений и ее решения.

Общая теория линейных систем дифференциальных уравнений.

Основные понятия и определения

При решении многих прикладных задач требуется найти функции , , …, , которые удовлетворяют системе уравнений, содержащих независимую переменную х, искомые функции , , …, и их производные, т.е. системе дифференциальных уравнений:

Говорят при этом, что система дифференциальных уравнений имеет порядок п ₁ относительно неизвестной у ₁, порядок п ₂ относительно у ₂, и т.д. Порядком системы называют число . Доказано, что всякую систему дифференциальных уравнений можно преобразовать к системе дифференциальных уравнений первого порядка:

Общую теорию систем дифференциальных уравнений и методы их интегрирования рассмотрим на примере системы двух дифференциальных уравнений первого порядка относительно двух неизвестных функций. Для удобства механической интерпретации такой системы независимую переменную обозначим t, а искомые функции – , . В этом случае система дифференциальных уравнений имеет вид

(1)

порядок этой системы равен сумме порядков её уравнений, т.е. равен двум.

Если в системе (4.1) каждое из уравнений разрешено относительно производной одной из неизвестных функций:

(2)

то говорят, что система дифференциальных уравнений записана в нормальной форме. Порядком нормальной системы дифференциальных уравнений называют число входящих в нее уравнений.

Определение 1

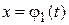Решением системы дифференциальных уравнений (1) (или (2)) называется любая пара непрерывно дифференцируемых на интервале функций , , которые при подстановке в систему обращают оба ее уравнения в тождества при всех .

Процесс нахождения решения системы дифференциальных уравнений называется интегрированием этой системы.

Определение 2

Пусть 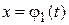, – решение системы дифференциальных уравнений (2) (или (4)). График решения, т.е. совокупность точек трехмерногопространства , t Î , называется интегральной кривой этой системы.

Определение 3

Задачей Коши для системы дифференциальных уравнений (2) называется задача отыскания решения , этой системы, удовлетворяющего начальным условиям

, , (3)

где – заданные числа.

Для системы (2) справедлива следующая теорема существования и единственности решения задачи Коши.

Теорема.1 (Коши)

Если функции и непрерывны вместе со своими частными производными по x и y в некоторой области D трехмерного пространства , то для любой внутренней точки 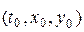ÎD существует единственное решение 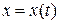, системы дифференциальных уравнений (2), удовлетворяющее условиям , .

Пусть D – область пространства переменных , в которой выполнены условия теоремы Коши.

Определение 4

Совокупность функций , , зависящих от произвольных постоянных , и непрерывно дифференцируемых по t, называется общим решением системы дифференциальных уравнений (2) в области D, если

1) эти функции удовлетворяют систем (2) при любых значениях постоянных С ₁, C ₂;

2) для любых начальных условий , , 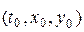ÎD, существуют такие значения постоянных , что функции , удовлетворяет этим начальным условиям:

, .

Определение 5

Решение , , полученное из общего решения , при конкретных значениях постоянных , называется частным решением системы дифференциальных уравнений (2).

Задача Коши, по существу, есть задача нахождения частного решения заданной системы дифференциальных уравнений. Геометрически – это задача отыскания интегральной кривой системы (2), проходящей через данную точку 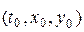пространства .

Рассмотрим нормальную систему дифференциальных уравнений

Независимую переменную t будем рассматривать как некоторый параметр (например, время), а совокупность значений функций

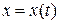, как прямоугольные декартовы координаты точки плоскости . Эту плоскость будем называть фазовой плоскостью (или фазовым пространством), точку – фазовой точкой, скорость движения этой точки – фазовой скоростью.

Пусть материальная точка М движется в плоскости . В механике уравнения движения обычно записывают в параметрической форме

где – координаты движущейся точки М в момент времени t, которые являются функциями времени t. Известно, что скорость движения (вообще говоря, переменная) характеризуется вектором . В общем случае, скорость движения зависит от времени и положения точки . Если эта зависимость известна, то имеем

(4)

Получили систему дифференциальных уравнений. Значит, уравнения системы устанавливают зависимость координат вектора скорости от времени t и положения точки на фазовой плоскости. Если рассматривать задачу Коши, то начальные условия , задают положение точки в начальный момент времени .

Таким образом, система дифференциальных уравнений (.4) определяет в фазовой плоскости множество векторов скоростей движущейся точки – векторное поле скоростей. Всякое решение

системы дифференциальных уравнений представляет собой закон движения точки, поэтому решение называют просто движением, определяемым системой (4). Уравнения движения определяют также и траекторию этого движения в фазовой плоскости – фазовую траекторию. При этом вектор скорости в каждой точке фазовой траектории совпадает с вектором заданного поля скоростей. Множество всех решений системы определяет множество фазовых траекторий, которые мы будем называть фазовым портретом системы дифференциальных уравнений. Не следует путать фазовые траетории и интегральные кривые системы дифференциальных уравнений: фазовые траектории представляют собой проекции интегральных кривых пространства на плоскость (рисунок 4.1).

В связи с такой механической интерпретацией системы дифферен­циаль­ных уравнений эту систему принято называть динамической.

Если в этих рассуждениях отвлечься от чисто механической природы движения и рассмотреть движение как некоторый процесс (эволюционный, работу прибора, радиоактивный распад, размножение бактерий и т.п.), то фазовое пространство есть множество состояний этого процесса (раньше состояние процесса называли фазой – отсюда и используемый термин). Значит, система дифференциальных уравнений определяет множество возможных состояний описываемого ею процесса.

Если система (4.4) такова, что в некоторой точке ее правые части равны нулю для всех рассматриваемых значений t, т.е.

то эта система имеет решение . Такое решение называется состоянием покоя или состоянием равновесия. Интегральная кривая этого решения – прямая, а фазовая траектория – точка (т.е. точка М на самом деле не движется, т.к. фазовые скорости равны нулю, рисунок 4.2). Точку называют точкой покоя или положением равновесия.

Из динамических систем наиболее важную роль играют автономные системы.

Если функции в системе дифференциальных уравнений (4.4) не зависят явно от t, то эта система называется автономной (стационарной):

Автономность системы означает, что закон изменения неизвестных функций, описываемый системой дифференциальных уравнений, не меняется с течением времени, что обычно и бывает с физическими законами. Иными словами, если

есть решение системы дифференциальных уравнений

то функции где t – const, также есть решение этой системы. Решения отличаются только сдвигом во времени, им соответствуют различные интегральные кривые, но одна и та же фазовая траектория (рисунок 4.3).

Для автономной системы поле скоростей стационарно (не меняется во времени) и движение является установившимся. Причем, если выполняются условия теоремы существования и единственности, то через каждую точку фазового пространства автономной системы проходит единственная фазовая траектория.

Линейные системы дифференциальных уравнений – общая теория

Наибольший интерес в силу обширности приложений представляют линейные системы дифференциальных уравнений, т.е. системы вида

(5)

где 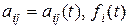– заданные функции, .

Если , 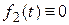для всех , то такая линейная система дифференциальных уравнений

(6)

называется однородной. В противном случае система (5) называется неоднородной.

Если все коэффициенты – действительные числа, то систему (5) (или (6)) называют линейной системой дифференциальных уравнений с постоянными коэффициентами. Теория линейных систем дифференциальных уравнений (свойства их решений, структура общего решения и специальные методы интегрирования) аналогична теории линейных дифференциальных уравнений. Ограничимся рассмотрением линейных систем с постоянными коэффициентами.

Пусть дана однородная линейная система дифференциальных уравнений (6) с постоянными коэффициентами. Два частных решения и этой системы называются линейно независимыми в интервале , если определитель

*)

для всех .

Фундаментальной системой решений (ФСР) системы линейных однородных дифференциальных уравнений называется совокупность двух линейно независимых решений { , } этой системы. Справедлива следующая теорема.

Теорема 2

Если система частных решений является фундаментальной, то общее решение системы (4.6) имеет вид

где – произвольные постоянные.

Не нашли, что искали? Воспользуйтесь поиском: