Метод Эйлера решения линейных однородных систем

Рассмотрим систему

Как следует из общей теории решения однородных линейных систем дифференциальных уравнений, общее решение системы имеет вид

где – фундаментальная системы решений, а – произвольные постоянные.

Рассмотрим метод построения фундаментальной системы решений, который называют методом Эйлера.

Частные решения, образующие фундаментальную систему решений, будем искать в виде

. (7)

Постоянные (числа и не равны нулю одновременно) находят из следующих условий.

I. Число является корнем уравнения

. (8)

Уравнение (8) называется характеристическим уравнением системы (6). Чтобы составить характеристическое уравнение, нужно:

1) записать матрицу из коэффициентов при неиз­вестных правой части системы (6);

2) составить матрицу . Матрицу называют характеристической матрицей системы;

3) вычислить определитель характеристической матрицы

=

и приравнять его к нулю .

Корни этого уравнения называют характеристическими корнями или характеристическими числами системы (6). Возможны три различных случая:

· корни характеристического уравнения действительные и различные;

· корни – действительные и равные;

· корни – комплексно-сопряженные.

В. Коэффициенты и в записи функций

являются решением системы

(.9)

где – корень характеристического уравнения. Такая алгебраическая система однородных линейных уравнений имеет бесконечное множество решений, но в задаче нахождения ФСР нужно взять одно ненулевое решение. При этом нужно ли составлять и решать систему (.9) для каждого из характеристических корней, зависит от вида этих корней.

а) Если корни характеристического уравнения действительные и различные, то, подставляя поочередно в систему (9) каждый из корней и решая ее, находим числа . В результате можно записать два частных решения системы (6):

,

.

Эти решения и образуют фундаментальную систему решений. В этом случае общее решение системы (6) имеет вид

б) Если корни характеристического уравнения комплексно-сопряженные: , то в систему (9) составляют и решают только для одного из этих чисел, например, . В этом случае решение системы также будет комплексным: , а соответствующее ему частное решение системы дифференциальных уравнений будет иметь вид

.

Чтобы построить фундаментальную систему решений, нужно отделить действительные и мнимые части этих комплексных функций. Для этого следует:

1) записать функцию в виде ;

2) подставить это в функции , и преобразовать:

,

;

3) отделить в этом решении действительные и мнимые части и записать два действительных линейно независимых частных решения системы дифференциальных уравнений, которые образуют фундаментальную систему решений:

и

,

Тогда общее решение системы (6) в случае комплексных корней характеристического уравнения имеет вид

в) Если корни характеристического уравнения действительные и равные: , то сразу находят общее решение системы (6), минуя непосредственное отыскание ФСР. Это решение отыскивают в виде

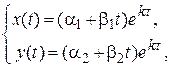(10)

где – некоторые неизвестные числа.

Подставляя эти функции в одно из уравнений системы (6) и преобразовывая полученные выражения, получают равенство двух многочленов первой степени относительно переменной t. Приравнивая коэффициенты при t и свободные члены этих многочленов, получают алгебраическую систему двух линейных однородных уравнений относительно неизвестных , , . Эта система имеет бесконечное множество решений и в рассматриваемом случае находят её общее решение*). Подставляя в (10) найденные значения , , , зависящее от произвольных постоянных , получают общее решение системы дифференциальных уравнений.

Из вышесказанного следует, что если характеристическое уравнение линейной однородной системы дифференциальных уравнений (6) имеет действительные и различные корни или комплексно-сопряженные корни, то для отыскания общего решения находим фундаментальную систему решений. Если же корни действительные и равные, то общее решение можно найти, не отыскивая ФСР. Поэтому начинать решение системы дифференциальных уравнений следует с нахождения корней характеристического уравнения.

Рассмотрим примеры.

Пример 1 Решить методом Эйлера систему дифференциальных

уравнений

Решение

Запишем матрицу из коэффициентов при неизвестных системы:

,

составим характеристическую матрицу

.

Тогда характеристическое уравнение имеет вид

.

Вычислим определитель

.

Тогда получим уравнение

,

корни которого , .

Получили два действительных и различных характеристических корня, поэтому будем искать фундаментальную систему решений в виде

;

(смотри условие В,a).

Для отыскания чисел составим систему вида (4):

и для каждого из чисел , найдем соответствующие ненулевые решения этой системы.

При имеем

Þ

Коэффициенты при неизвестных этой системы пропорциональны, поэтому она равносильна одному из уравнений этой системы, например

*).

Это уравнение имеет бесконечно много ненулевых решений. Перепишем его в виде . Положив, например, , получим . Тогда . Следовательно, первое решение фундаментальной системы, соответствующее корню , имеет вид

, .

При имеем

Þ

Система равносильна одному уравнению , откуда . Положив , получим , значит, . Соответствующее корню решение фундаментальной системы имеет вид

, .

Используя полученную фундаментальную систему , запишем общее решение системы в виде

В нашем случае получим

Ответ:

Пример 2 Решить методом Эйлера систему

Решение. Характеристическая матрица системы имеет вид

.

Тогда характеристическое уравнение:

Þ Þ .

Решая это уравнение, получаем

.

Таким образом, характеристическое уравнение имеет комплексно-сопряженные корни , (случай В,б), где ).

Составим систему вида (4.9):

и найдем её ненулевое решение для одного из корней характеристического уравнения. Подставив в эту систему, например, , получим

Поскольку определитель этой системы равен нулю (число – корень характеристического уравнения), то одно из уравнений системы является следствием другого*). Поэтому система равносильна одному из её уравнений. Возьмем, например, второе уравнение и решим его:

, или .

Отсюда имеем , . Полагая здесь , получим .

Тогда соответствующее комплексное решение системы дифференциальных уравнений имеют вид

.

Чтобы построить фундаментальную систему решений, отделим действительные и мнимые части этих комплексных функций. Для этого вначале запишем

.

Подставим полученное выражение в функции , и преобразуем:

,

.

Отделив в этих функциях действительные и мнимые части, получим две пары функций, образующие фундаментальную систему решений заданной системы дифференциальных уравнений:

, ,

, .

Значит, общее решение системы имеет вид

Ответ:

Пример 3 Решить систему

Решение. Находим корни характеристического уравнения:

Þ Þ Þ .

Так как корни равные, то будем искать сразу общее решение системы в виде

(à)

где – подлежащие определению числа. Чтобы их найти, используем тот факт, что функции являются решением заданной системы дифференциальных уравнений, и значит, удовлетворяют каждому из уравнений системы.

Подставим функции (à) в первое уравнение заданной системы. Для этого вначале найдем производную функции :

.

В результате подстановки получим:

Þ .

Преобразуем левую и правую части этого равенства:

,

,

.

Получили равенство двух многочленов первой степени относительно переменной t. Приравнивая коэффициенты при t, и свободные члены этих многочленов, получим:

или

Получили алгебраическую систему двух линейных однородных уравнений с четырьмя неизвестными , , . Легко убедиться в том, что ранг основной матрицы этой системы равен двум, значит, система имеет множество решений. Запишем ее в виде

Полагая здесь , , где – произвольные постоянные, запишем общее решение этой системы

Подставляя найденные значения , , в (à), получим общее решение заданной системы дифференциальных уравнений:

Ответ:

Метод исключения

Рассмотрим метод интегрирования систем линейных дифференциальных уравнений, называемый методом исключения. Этот метод состоит в сведении системы к одному или нескольким линейным дифференциальным уравнениям с одной неизвестной функцией в каждом.

Проиллюстрируем этот метод на примерах.

Пример 5 Решить методом исключения систему дифференциальных уравнений

Решение

Преобразуем заданную систему уравнений к дифференциальному уравнению от одной из неизвестных функций. Для этого удобно из первого уравнения системы выразить у через и :

. (à)

Продифференцируем обе части этого равенства:

.

Подставим эти выражения для и у во второе уравнение системы:

Þ . (àà)

Получили линейное однородное дифференциальное уравнение второго порядка относительно функции . Чтобы найти общее решение этого уравнения, найдем фундаментальную систему решений. Характеристическое уравнение имеет корни:

.

Следовательно, общее решение уравнения (àà) имеет вид

.

Чтобы определить функцию , используем равенство (à). Найдем

и подставим в равенство (à). Получим

.

Таким образом, общее решение системы дифференциальных уравнений имеет вид

Ответ:

Пример.6 Решить систему линейных дифференциальных уравнений

Решение: Из второго уравнения выразим *):

, откуда .

Подставим эти выражения для х и в первое уравнение системы и преобразуем:

, , .

Получили линейное однородное дифференциальное уравнение второго порядка относительно неизвестной функции . Найдем общее решение этого уравнения.

Корни характеристического уравнения:

Þ .

Отсюда общее решение дифференциального уравнения имеет вид

.

Найдем функцию . Имеем

.

Тогда

=

.

Итак, общее решение данной системы имеет вид

Ответ: .

Пример 7 Решить методом исключения

Решение

Из первого уравнения системы выразим у:

,

откуда . Подставляя эти выражения для у и у ¢ во второе уравнение системы, получим

,

.

Получили линейное неоднородное дифференциальное уравнение второго порядка, правая часть которого имеет специальный вид (таблица 3.3, II, стр.59).

Общее решение этого уравнения будем искать в виде

,

где – общее решение соответствующего линейного однородного дифференциального уравнения, а 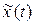– какое-либо частное решение рассматриваемого уравнения. Найдем каждое из этих решений.

Соответствующее однородное дифференциальное уравнение имеет вид

.

Найдем его общее решение . Корни характеристического уравнения:

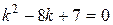Þ .

Тогда .

Частное решение 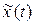дифференциального уравнения подберем по виду его правой части

.

Очевидно, это – функция типа где – многочлен нулевой степени, а число не является корнем характеристического уравнения. Значит, частное решение будем искать в виде

,

где А – неизвестный числовой коэффициент. Для его вычисления найдем производные от функции :

,

и подставим все эти выражения в уравнение вместо неизвестной х и ее производных:

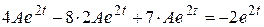, откуда , .

Значит, , а общее решение уравнения имеет вид

.

Теперь найдем вторую неизвестную функцию , используя соотношение

.

Для этого найдем производную функции :

.

Тогда

.

Таким образом, общее решение системы имеет вид

Ответ: .

*) Определитель называется определителем Вронского для системы функций

*) Доказано, что ранг такой системы, полученной в процессе решения рассматриваемой задачи, равен двум, поэтому её общее решение содержит две произвольные постоянные.

*) В подобных случаях рекомендуем выбирать наиболее простое из уравнений полученной системы, т.е. с меньшими коэффициентами.

*) В этом легко убедиться, умножив, например, первое уравнение на число.

*) Заметим, что можно было бы выразить через и из первого уравнения.

Не нашли, что искали? Воспользуйтесь поиском: