Лекции 5. Основные теоремы дифференциального исчисления. Приложения производных к исследованию функции

Содержание лекции: теоремы о дифференцируемых функциях: Ролля, Лагранжа. Формула Тейлора. Правило Лопиталя.

Монотонность функции. Точки экстремума. Наибольшее и наименьшее значения функции на отрезке.

Выпуклость, вогнутость графика функции, точки перегиба.

1. Теоремы о дифференцируемых функциях. Правило Лопиталя

Теорема 5.1(Ролля)

Пусть функция f (x) определена и непрерывна на [ a; b ], дифференцируема, по крайней мере, на (а; b), а на концах отрезка принимает равные значения: f (a) = f (b). Тогда существует хотя бы одна точка с Î(a; b) такая, что f ¢(c) = 0.

Сравните эту теорему с I теоремой Больцано-Коши (теорема 3.5). Там речь шла о существовании нуля функции, а здесь – о нуле производной.

Доказательство. 1) Если f (x) = const на [ a; b ], то условие f (a) = f (b) выполняется с очевидностью. Но и f ¢(x) = (const)¢ = 0 также выполняется, причем " х Î[ a; b ].

2) Пусть f (x) ¹ const на [ a; b ]. Так как функция f (x) непрерывна на отрезке, то, согласно теореме Вейерштрасса (теорема 3.7), она достигает на нем наименьшего т и наибольшего М значений. Очевидно М >т. Причем эти значения не могут достигаться на концах отрезка, т.к. f (a) = f (b). Значит, хотя бы одно из них достигается во внутренней точке с Î[ a; b ].Для определенности положим f (c) = т. Так как функция f (x) дифференцируема в интервале(a; b), то в точке с существует конечная производная:

.

Так как f (c) = т – наименьшее значение функции, то f (c + D x) – f (c)³0 для всех х ¹ с и для любого D x. Значит, 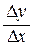³ 0 при D x > 0 и 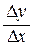£ 0 при D x < 0. Но тогд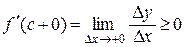а

, а .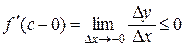

Поскольку функция в точке х = с имеет конечную производную, то

f ¢(c) = f ¢(c +0) = f ¢(c –0),

а это возможно лишь при условии f ¢(c) = f ¢(c +0) = f ¢(c –0) = 0. ЧТД.

С геометрической точки зрения Теорема Ролля означает: если крайние ординаты точек кривой равны, то на кривой найдется, по крайней мере, одна точка, в которой касательная горизонтальна (рис. 1).

Теорема 5.2.(Лагранжа)

Пусть функция f (x) определена и непрерывна на [ a; b ] и дифференцируема, по крайней мере, на (а; b). Тогда существует хотя бы одна точка с Î(a; b) такая, что

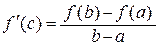, или f (b) – f (a) = f ¢ (c)(b – a).

Доказательство. Рассмотрим вспомогательную функцию

j(х) = f (х) – f (a) – 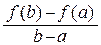(х – a).

Эта функция удовлетворяет всем условиям теоремы Ролля. Действительно, j(х) определена и непрерывна на [ a; b ]. На (а; b) эта функция дифференцируема, так как составлена из дифференцируемых функций f (x) и линейной функции 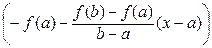, которая определена, непрерывна и дифференцируема на любом отрезке. Кроме того,

j(а) = j(b) = 0.

Значит, согласно теореме Ролля, найдется хотя бы одна точка с Î(a; b), такая, что j¢(с) = 0. Но тогда

j ¢(с) = f ¢(с) – 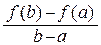= 0, откуда 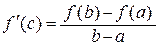. ЧТД.

Рассмотрим геометрический смысл этой теоремы. Заметим сначала, что

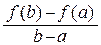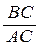= = tgb (рис. 2) – т.е. угловому коэффициенту хорды АВ.

Но f ¢(с) = tga – угловому коэффициенту касательной, проведенной к графику функции в точке (с, f (c)).

Из равенства 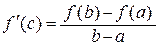следует равенство tgb = tga, которое означает, что касательная и хорда имеют одинаковый наклон, т.е. параллельны между собой. Таким образом, теорема Лагранжа утверждает, что найдется хотя бы одна точка, в которой касательная была бы параллельно хорде.

Теорема 5.3

Если функция 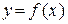в некоторой окрестности точки 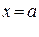имеет производные до 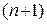-го порядка включительно, то для любого х из этой окрестности справедлива формула Тейлора (п -го порядка):

.

Здесь слагаемое называется остаточным членом и может быть вычислено по формуле , а точка x лежит между точками х и а (можно записать , ).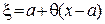

Формула Тейлора позволяет представить приближенно (аппроксимировать) произвольную функцию 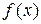в виде многочлена:

.

Многочлен в правой части этого равенства называют многочленом Тейлора. Остаточный член (который в этом приближенном равенстве отсутствует) определяет погрешность аппроксимации.

При 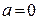получаем частный случай формулы Тейлора – формулу Маклорена:

,

где , .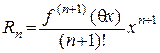

Теорема 5.4.(Правило Лопиталя)

Пусть функции f (x) и g (x) определены и дифференцируемы в окрестности точки х ₀, причем g ¢(x ₀) ¹ 0. Если 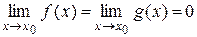(или ¥) и существует (конечный или бесконечный) 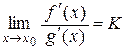, то существует и .

Теорема 5.4 позволяет вычисление предела отношения двух функций, в случае неопределенности 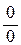или , свести к вычислению предела отношения их производных.

Пример: 1) .

2) .

Не нашли, что искали? Воспользуйтесь поиском: