
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Наибольшее и наименьшее значения функции на отрезке.
Как уже отмечалось, понятие экстремума носит локальный характер, т.е. связано с некоторой окрестностью соответствующей точки. Но если функция непрерывна на отрезке [ a; b ], то, по теореме Вейерштрасса, на этом отрезке она достигает своего наибольшего и наименьшего значения:
$ х 1, х 2Î[ a; b ]: f (x 1) £ f (x) £ f (x 2) " х Î[ a; b ].

 Нетрудно понять, что эти значения достигаются либо в точках экстремума функции, принадлежащих этому отрезку, либо в граничных точках отрезка (рис.5).
Нетрудно понять, что эти значения достигаются либо в точках экстремума функции, принадлежащих этому отрезку, либо в граничных точках отрезка (рис.5).
|
Следовательно, чтобы найти наибольшее и наименьшее значения функции f (x) (их называют глобальными экстремумами) на отрезке [ a; b ], нужно:
1) выяснить, содержится ли данный отрезок в области определения функции;
2) найти критические точки функции, принадлежащие этому отрезку и вычислить значение функции в этих точках;
3) Найти f (а) и f (b);
4) Сравнить все найденные значения функции и выбрать среди них наибольшее и наименьшее. Обозначают эти значения f наиб. и f наим. или 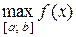 и
и  соответственно.
соответственно.
В случае, если глобальный экстремум ищется на интервале (а, b), или на полуинтервале [ а, +¥), или (–¥, b ], то нужно вместо f (а), f (b) вычислить соответствующий предел.
Пример:
Найти наибольшее и наименьшее значения функции f (x) = хе –2 х на промежутке [–1, +¥).
Действуя по приведенному алгоритму, имеем
1) Область определения данной функции (-¥; +¥). Очевидно,
[–1, +¥)Ì(-¥; +¥).
2) Найдём критические точки и значения функции в них:
f¢ (x) = (хе –2 х )¢ = е –2 х –2 хе –2 х = е –2 х (1 – 2 х) = 0 Þ 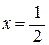 Î [–1, +¥), и
Î [–1, +¥), и
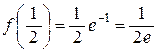 ;
;
3) Найдём значения функции на концах промежутка:
f (– 1) = – е 2,
f (+¥) = 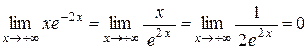 .
.
4) Сравним найденные значения: 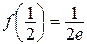 ,
,  , f (+¥)=0. Очевидно,
, f (+¥)=0. Очевидно, 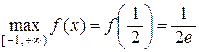 ,
,  .
.
Заметим, что если бы значение f (+¥) было бы меньше f (– 1) = – е 2, то ответ был бы таков: наименьшего значения функция на этом промежутке не достигает. Аналогично, если бы f (+¥) > 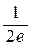 , то функция не достигала бы на данном промежутке наибольшего значения.
, то функция не достигала бы на данном промежутке наибольшего значения.
4. Выпуклость, вогнутость графика функции, точки перегиба.
Знак первой производной функции y = f (x) определяет характер роста функции: f ¢(х) > 0 Þ f (х) возрастает, f ¢(х)< 0 Þ f (х) убывает. Но и знак второй производной так же влияет на характер изменения функции.
 Действительно, рассмотрим кривую y = f (x). Если f ¢¢(x) = (f ¢(x))¢ > 0, то производная f ¢ возрастает, значит, угол наклона касательной к кривой y = f (x) растёт – касательная поворачивается против часовой стрелки, а кривая изгибается вниз и лежит выше касательных, в этом случае кривую называют вогнутой (рис.6а).
Действительно, рассмотрим кривую y = f (x). Если f ¢¢(x) = (f ¢(x))¢ > 0, то производная f ¢ возрастает, значит, угол наклона касательной к кривой y = f (x) растёт – касательная поворачивается против часовой стрелки, а кривая изгибается вниз и лежит выше касательных, в этом случае кривую называют вогнутой (рис.6а).
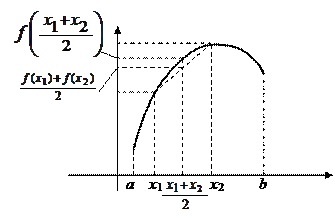 Если f ¢¢(x) = (f ¢(x)¢ < 0, то f ¢ убывает, значит, убывает угол наклона касательной, кривая изгибается вверх и лежит ниже касательных. Эта кривая выпуклая (рис.6б).
Если f ¢¢(x) = (f ¢(x)¢ < 0, то f ¢ убывает, значит, убывает угол наклона касательной, кривая изгибается вверх и лежит ниже касательных. Эта кривая выпуклая (рис.6б).
В общем случае функция y = f (x) называется выпуклой на отрезке [ a, b ], если " x 1, x 2Î[ a, b ] выполняется
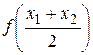 ³
³  .
.
Но поскольку это определение не наглядно, то рассмотрим такое
Определение 5.2
Кривая y = f (x) (и функция f (x) в том числе) называется выпуклой (выпуклой вверх) на [ a, b ] если она расположена ниже любой своей касательной.
Кривая y = f (x) (а так же функция f (x)) называется вогнутой (выпуклой вниз) на [ a, b ], если она расположена выше любой своей касательной.

Определение 5.3
|
 кривой y = f (x) называется точкой перегиба этой кривой (или функции f (x)), если при переходе через эту точку меняется направление выпуклости кривой.
кривой y = f (x) называется точкой перегиба этой кривой (или функции f (x)), если при переходе через эту точку меняется направление выпуклости кривой.
Теорема 5.9 (необходимое и достаточное условие выпуклости)
Пусть f (x) непрерывна и дважды дифференцируема на (a, b). Для того чтобы, кривая y = f (x) была выпуклой (вогнутой) на (a, b), необходимо и достаточно, чтобы " x Î(a, b) f ¢¢ (x) > 0 (f ¢¢ (x) < 0 соответственно).
Теорема 5.10. (необходимое условие точки перегиба)
Если (x 0, f (x 0)) – точка перегиба кривой y = f (x), то f ¢¢ (x 0) равна нулю или не существует.
 Точки x 0Î [ a, b ], в которой f ¢¢ (x 0) = 0 или не $, называются критическими точками 2-го рода функции y = f (x). Не всякая критическая точка определяет точку перегиба.
Точки x 0Î [ a, b ], в которой f ¢¢ (x 0) = 0 или не $, называются критическими точками 2-го рода функции y = f (x). Не всякая критическая точка определяет точку перегиба.
Например: у = x 4, y ¢= 4 x 3, y ¢¢ = 12 x 2, значит, x = 0 – критическая точка, но перегиба в этой точке график функции не имеет.
Но из определения точки перегиба и теоремы 5.10 следует достаточное условие точки перегиба кривой.
Теорема 5.11. (достаточное условие точки перегиба)
Критическая точка x 0 есть абсцисса точки перегиба (x 0, f (x 0) кривой  , если при переходе через эту точку f ¢¢(x) меняет знак.
, если при переходе через эту точку f ¢¢(x) меняет знак.
Алгоритм исследования выпуклости и точек перегиба
1. Найти область определения D(f) функции f (x);
2. Найти критические точки xi второго рода: f ¢¢ (xi) = 0 или не $;
3. Определить знак f ¢¢ (x) в каждом из интервалов, на которые критические точка xi разбивают D(f).
4. Там, где f ¢¢ (x) > 0, кривая y = f (x) вогнутая, где f ¢¢ (x) < 0 – выпуклая;
5. Точки xk, при переходе через которые меняется знак f ¢¢ (x), есть абсциссы точек перегиба. Найти f (xk), записать координаты точек перегиба (xk, f (xk)) графика функции.
Общая схема исследования функции.
Мы рассмотрели характерные особенности изменения функции и ее графика, а так же способы изучения этих особенностей. Эта теория может быть использована при полном исследовании функции с целью подробного построения ее графика.
Общая схема исследования функции y = f (x) и построение её графика включает следующие этапы:
1. Область определение функций D(f).
2. Свойства: чётность, нечётность, симметрия, график, периодичность
3. Точки пересечения с осями координат, интервалы знакопостоянства (y >0, y < 0).
4. Непрерывность, классификация точек разрыва.
5. Асимптоты графика.
6. Интервалы монотонности, точки экстремума.
7. Интервалы выпуклости, точки перегиба.
8. Построение графика.
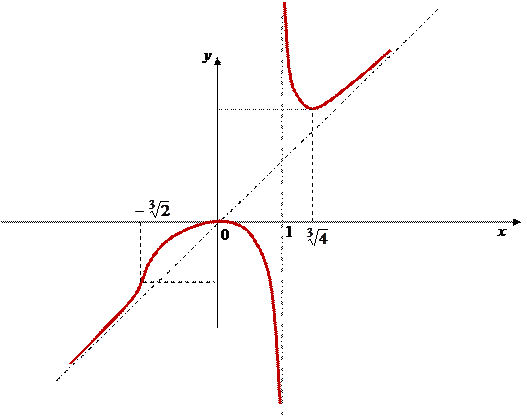
Пример: Исследовать функцию  и построить ее график.
и построить ее график.
Решение. Придерживаемся указанного алгоритма.
1. D (f) = (-¥; 1)È(1; ¥)
2. D (f) – не симметрична Þ функция не является ни четной, ни нечетной. Функция не периодическая, т.к. не имеет тригонометрических составляющих.
3. Пересечение с OX Þ y = 0, 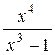 = 0 Þ x = 0, точка (0, 0) есть точка пересечения с ОХ.
= 0 Þ x = 0, точка (0, 0) есть точка пересечения с ОХ.
Пересечение с OYÞ x = 0 Þ y = 0 – та же точка (0, 0).
4. Так как y=  - элементарная, то область ее непрерывности совпадает с областью определения D(f), тогда x = 1 – точка разрыва. Находим
- элементарная, то область ее непрерывности совпадает с областью определения D(f), тогда x = 1 – точка разрыва. Находим
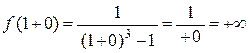 ,
,
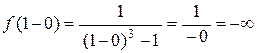 ,
,
значит, x =1– точка разрыва II рода (бесконечного разрыва).
5. Из предыдущего пункта следует, что x = 1 – вертикальная асимптота графика данной функции. Найдем наклонные асимптоты:
k =  =1, b =
=1, b =  =0,
=0,
значит, y = x – наклонная асимптота.
6. Найдем интервалы монотонности и экстремумы:
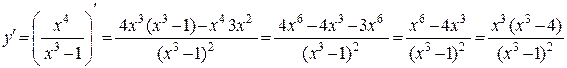 ,
,
Тогда у ¢ = 0 Þ 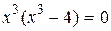 , откуда x = 0,
, откуда x = 0,  ;
;
y ¢ не существует при х =1 Ï D(f).
Область определения функции этими точками разбивается на 4 интервала, определим знак производной на каждом из этих интервалов (взяв, например промежуточные точки х= -1, х =0,1, х =1,1, х =2 и вычислив в этих точках значения у ¢). Получим:

Значит, x = 0 – точка max, ymax=y (0) = 0; x = 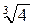 – точка min, y (
– точка min, y ( ) =
) =  .
.
На интервалах (– ¥, 0) и (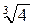 ,+¥) функция возрастает, а на интервалах (0, 1) и (1,
,+¥) функция возрастает, а на интервалах (0, 1) и (1, 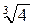 ) функция убывает.
) функция убывает.
7. Найдем интервалы выпуклости, вогнутости, точки перегиба графика функции.
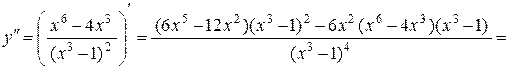
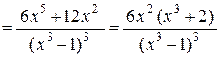 ,
,
откуда у ¢¢ = 0 при x = 0 и 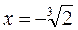 , y ¢¢ не существует при x =1Ï D(f).
, y ¢¢ не существует при x =1Ï D(f).
Эти точки разбивают область определения функции на 4 интервала. Определяем знак у ¢¢ на каждом из них, взяв, например, промежуточные точки х =-2, х =-1, х =0,5, х =2 и вычислив в этих точках значения у ¢¢. Получим:
 |
При переходе через точку 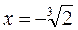 вторая производная меняет знак, следовательно,
вторая производная меняет знак, следовательно, 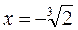 - абсцисса точки перегиба. Находим
- абсцисса точки перегиба. Находим
y 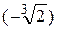 =
= 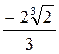 ,
,
значит, точка (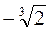 ,
, 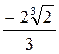 ) – точка перегиба. Других точек перегиба нет.
) – точка перегиба. Других точек перегиба нет.
На интервалах (– ¥, 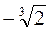 ) и (1, +¥) график функции вогнутый.
) и (1, +¥) график функции вогнутый.
На интервале (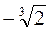 , 1) – график выпуклый.
, 1) – график выпуклый.
8. Сведем полученные результаты в таблицу:
| X | (-¥; 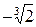 ) )
| 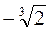
| (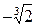 ; 0) ; 0)
| (0, 1) | (1; 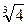 ) )
| 
| (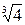 ;¥) ;¥)
| |
| у ¢ | + | - | + | - | - | + | ||
| у ¢¢ | + | - | - | + | + | |||
| у |  у ® у = х при х ® –¥ у ® у = х при х ® –¥
| 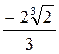
| 
|  у (1–0)=–¥
у (1–0)=–¥
|  у (1+0)=+¥
у (1+0)=+¥
| 
|  у ® у = х при х ® +¥ у ® у = х при х ® +¥
|
По этим данным построим график функции.
 |
Не нашли, что искали? Воспользуйтесь поиском: