
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Уравнение движения вращающегося тела
Уравнение движения материальной точки связывает, как мы знаем, скорость изменения ее импульса с действующей на нее силой. Поступательное движение твердого тела мало чем отличается от движения материальной точки и уравнение этого движения заключается в такой же связи между полным импульсом тела 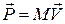 и полной действующей на него силой
и полной действующей на него силой 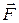 :
:
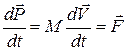 (12)
(12)
Для вращательного движения аналогичную роль играет уравнение, связывающее скорость изменения момента импульса тела с моментом действующих на него сил. Выясним, как выглядит эта связь, причем снова ограничимся простейшим случаем вращения тела вокруг определенной закрепленной оси (ось Z).
Момент импульса тела относительно оси вращения мы уже определили. Обратимся теперь к действующим на тело силам. Ясно, что силы, направленные параллельно оси вращения, могут только сдвинуть тело вдоль этой оси, но не могут произвести вращения тела. Мы можем поэтому не принимать во внимание таких сил и рассматривать только силы, лежащие в плоскости, перпендикулярной оси вращения.
Момент Nz такой силы 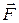 относительно оси Z дается величиной векторного произведения
относительно оси Z дается величиной векторного произведения  , где
, где  — вектор расстояния точки приложения силы от оси. По определению векторного произведения имеем
— вектор расстояния точки приложения силы от оси. По определению векторного произведения имеем
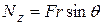 (13)
(13)
где 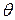 — угол между
— угол между 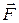 и
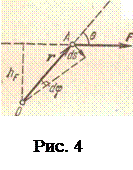
и  (на рис. 4 ось Z перпендикулярна плоскости чертежа и проходит через точку О; А есть точка приложения силы). Иначе можно записать
(на рис. 4 ось Z перпендикулярна плоскости чертежа и проходит через точку О; А есть точка приложения силы). Иначе можно записать
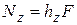 (15)
(15)
где 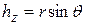 — плечо силы относительно оси (расстояние от оси до направления действия силы).
— плечо силы относительно оси (расстояние от оси до направления действия силы).
Согласно взаимосвязи между скоростью изменения момента импульса и моментом действующих сил можно написать теперь равенство
 или
или 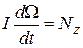 (16)
(16)
Это и есть уравнение движения вращающегося тела. Производную  можно назвать угловым ускорением. Мы видим, что оно определяется моментом действующей на тело силы, подобно тому как ускорение поступательного движения определяется самой силой.
можно назвать угловым ускорением. Мы видим, что оно определяется моментом действующей на тело силы, подобно тому как ускорение поступательного движения определяется самой силой.
Если на тело действует несколько сил, то под Nz в написанном уравнении следует, конечно, понимать сумму их моментов. При этом надо помнить о векторном происхождении величины Nz и приписывать разные знаки моментам сил, стремящимся повернуть тело в противоположных направлениях вокруг оси. Положительный знак имеют моменты сил, под действием которых тело поворачивается в направлении, отвечающем условленному направлению отсчета угла j поворота тела вокруг оси (j есть тот угол, производная которого по времени есть угловая скорость вращения тела: 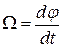 ).
).
Отметим также, что в твердом теле можно, не изменяя свойств движения, любым образом смещать точку приложения силы вдоль направления ее действия. Очевидно, что такой перенос не изменит плеча силы, а потому не изменится и ее момент.
Условие равновесия тела, могущего вращаться вокруг некоторой оси, заключается, очевидно, в равенстве нулю суммы моментов действующих на него сил. Это — так называемый закон моментов. Его частным случаем является известное правило рычага, устанавливающее условие равновесия стержня, могущего вращаться вокруг одной из своих точек.
Существует простая связь между моментом действующей на тело силы и работой, производимой ею при вращении тела. Работа, производимая силой 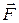 при повороте тела вокруг оси на бесконечно малый угол dj (рис. 4), равна произведению перемещения ds=rdj точки А приложения силы на составляющую FS=Fsinq силы вдоль направления движения:
при повороте тела вокруг оси на бесконечно малый угол dj (рис. 4), равна произведению перемещения ds=rdj точки А приложения силы на составляющую FS=Fsinq силы вдоль направления движения:
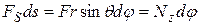 (17)
(17)
Мы видим, что момент силы относительно оси совпадает с производимой ею работой, отнесенной к единичному угловому перемещению. С другой стороны, произведенная над телом работа равна убыли его потенциальной энергии. Поэтому можно написать, что  откуда
откуда
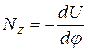 (18)
(18)
Таким образом, момент силы равен взятой с обратным знаком производной от потенциальной энергии по углу поворота тела вокруг данной оси. Обратим внимание на аналогию между этим соотношением и формулой  , связывающей саму силу с изменением потенциальной энергии при движении материальной точки или при поступательном перемещении тела.
, связывающей саму силу с изменением потенциальной энергии при движении материальной точки или при поступательном перемещении тела.
Легко убедиться в том, что уравнение движения вращающегося тела находится, как и должно было быть, в согласии с законом сохранения энергии. Полная энергия тела есть
 (19)
(19)
а ее сохранение выражается равенством
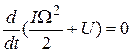 (20)
(20)
По правилу дифференцирования функции от функции имеем
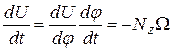 (21)
(21)
Производная же 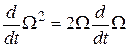 . Подставив эти выражения и сократив общий множитель
. Подставив эти выражения и сократив общий множитель 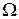 , мы снова получим известное уже нам уравнение
, мы снова получим известное уже нам уравнение
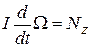 (22)
(22)
Если применить соотношение 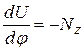 к внутренней потенциальной энергии системы, понимая при этом под Nz суммарный момент действующих на все ее частицы сил, то мы увидим, что условие неизменности потенциальной энергии при повороте замкнутой системы вокруг любой оси действительно означает равенство нулю суммарного момента сил.
к внутренней потенциальной энергии системы, понимая при этом под Nz суммарный момент действующих на все ее частицы сил, то мы увидим, что условие неизменности потенциальной энергии при повороте замкнутой системы вокруг любой оси действительно означает равенство нулю суммарного момента сил.
Не нашли, что искали? Воспользуйтесь поиском: