Тождества алгебры логики

1. А • В = В • А;

A ∨ B = B ∨ A.

Тождества 1 устанавливают, что в суждениях с союзами, являющимися конъюнкцией и дизъюнкцией, члены конъюнкции и дизъюнкции можно переставлять.

2. А • (В • С) = (А • В) • С;

A ∨ (B ∨ C) = (A ∨ B) ∨ C.

Эти тождества устанавливают, что последовательность применения к суждениям одной и той же операции “•” или “∨” может быть любой. Правильность этих тождеств очевидна, поскольку в естественном языке скобки в таких случаях вообще не употребляются.

3.А • (В ∨ C) =A • В ∨ A • С;

А ∨ (В • С) = (А ∨ В) • (А ∨ С).

Знак “•” здесь связывает теснее, чем “∨”.

В элементарной алгебре есть аналог первого из этих тождеств:

а • (в+с) = (а • в) + (а • с);

аналога второго из них тождеств нет, так как равенство:

а+(в • с) = (а+в) • (в+с) неверно в элементарной алгебре.

Пример суждений, тождественных в силу первого из тождеств 3: “Петров знает английский язык, и он знает французский или немецкий”, “Петров знает английский и французский языки или Петров знает английский и немецкий языки”. Если тождество не кажется очевидным, то его можно проверить при помощи таблицы истинности.

4. А • А = А;

А ∨ А= А.

На основе тождества 4 повторения в сложных суждениях можно сократить.

Отрицая ложь, получим истину, и наоборот.

В главе V в качестве переменных для суждений использовались символы р, q, r, s и эти же символы с нижними индексами. В том же значении эти символы будут употребляться и в этой главе. Последовательность символов, получаемую в результате замены простых суждений, входящих в сложное суждение, пропозициональными переменными, а союзов “и” и “или” — символами “•” и “∨”, отрицания — символом “-”, будем называть формулой. Например, суждению "Понятые не приглашены или протокол не составлен" соответствует формула:

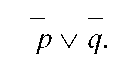
Формулами являются также пропозициональные переменные и символы 1 и 0.

На основе тождеств 1—13 можно преобразовывать формулы. Например, из формулы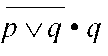

можно получить тождественную ей формулу 0 следующим образом:

Установлено, что исходная формула тождественна 0, то есть суждение, которому эта формула соответствует, является ложным.

Из того как использовались тождества 1—13 можно уяснить, что в них буквами А, В, С обозначаются формулы.

Построенная алгебра имеет и другие интерпретации.

Рассмотрим одну из таких возможных интерпретаций. Пусть буквами А, В, С обозначаются объемы понятий (классы предметов), а символами “•”, “v”, “-”соответственно операции пересечения, объединения классов, дополнения к классу в некотором универсуме.

Пересечением классов А и В называется новый класс А • В, элементами которого являются те и только те предметы, которые принадлежат как классу А, так и классу В. Графически этот класс изображается заштрихованной частью кругов А и В:

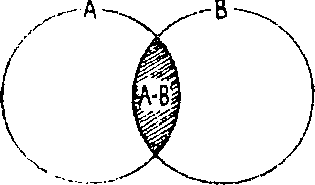
Объединением классов А и В называется новый класс A ∨ В, элементами которого являются все элементы классов А и В. Графически этот класс

представляется заштрихованной поверхностью круговой схемы:

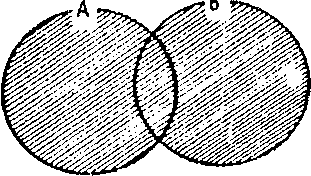
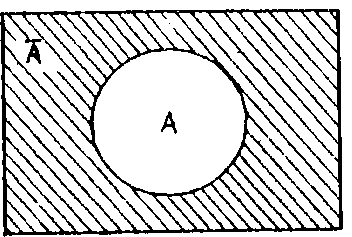
Пусть нулем обозначается нулевой (пустой) класс, а единицей — универсальный, то есть класс, включающий все предметы исследуемой области. Тогда дополнением к классу А в универсальном классе называется класс А, элементами которого являются все элементы универсального класса, за исключением элементов класса А. Обозначим на схеме универсальный класс прямоугольником. Класс А представляется заштрихованной поверхностью.

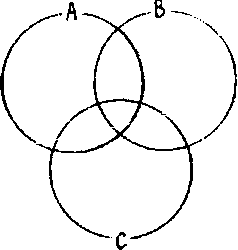
Для иллюстрации первого из тождеств 3 посредством этой интерпретации начертим три пересекающихся круга А, В, С.

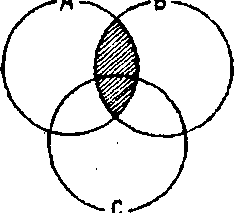
Чтобы получить класс А • (B ∨ C), сначала осуществим объединение классов В и С.

Класс B ∨ C представлен заштрихованной поверхностью круговой схемы. Теперь осуществим пересечение классов А и B ∨ C:

В результате получим класс А•(B∨C), представленный поверхностью круговой схемы, заштрихованной дважды.

Затем начертим еще три пересекающихся круга А, В, С. Для графического изображения класса A•B∨A•C (правой части первого из тождеств

3) представим сначала графически класс АВ:

Затем представим графически класс А•С:

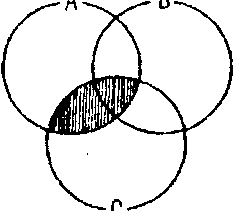
Объединение классов А•В и А•С представляется заштрихованной поверхностью схемы:

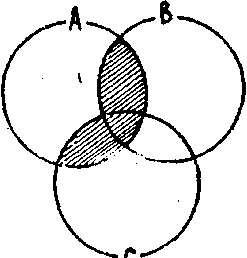
При этом оказывается, что классы А•(B∨C) и A•B∨A•C совпадают, что подтверждает правильность первого из тождеств 3.

Предлагаем читателю самостоятельно обосновать правильность второго из тождеств 3 описанным способом.

Не нашли, что искали? Воспользуйтесь поиском: