
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
С. Другие применения алгебры логики
1. Символическая логика, в том числе алгебра логики, широко применяется в кибернетике. Об отце символической логики Лейбнице Норберт Винер, сформулировавший основные идеи кибернетики, пишет: “Если бы мне пришлось выбирать в анналах истории наук святого — покровителя кибернетики, то я выбрал бы Лейбница. Философия Лейбница концентрируется вокруг двух идей, тесно связанных между собой: идеи универсальной символики и идеи логического исчисления.
Из этих двух идей возникли современный математический анализ и современная математическая логика. И как в арифметическом исчислении была заложена возможность развития ее механизации от абака и арифмометра до современных сверхбыстрых машин, так и в исчислении умозаключений Лейбница содержится в зародыше думающая машина. Сам Лейбниц, подобно своему предшественнику Паскалю, интересовался созданием вычислительных машин в металле. Поэтому совсем неудивительно, что тот же самый умственный толчок, который привел к развитию математической логики, одновременно привел к гипотетической или действительной механизации процессов мышления”[68].
2. Алгебра логики применяется при проектировании переключательных схем, являющихся элементами автоматизированных систем управления и вычислительных машин. При этом символ “•” интерпретируется как последовательное соединение переключателей, а символ “∨” — как параллельное. Например, формулам p • (q ∨ r) и р • q ∨ р • r соответствуют следующие схемы:
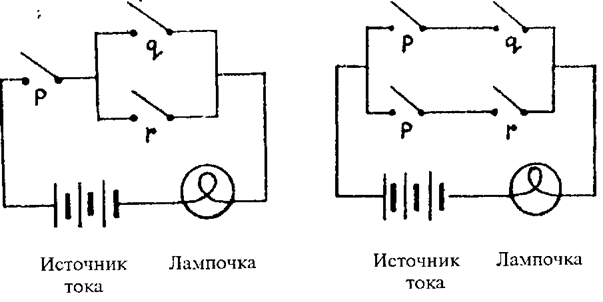
р = 1 — переключатель замкнут, р = 0 — разомкнут. Если в схеме имеются два (или более) переключателя р, то они могут быть замкнуты (или разомкнуты) только одновременно (именно поэтому они обозначаются одной и той же буквой).
По электрической цепи, изображенной на левой схеме, ток идет тогда и только тогда, когда он идет по цепи, изображенной на правой схеме, так как формулы р • (q ∨ r) и р • q ∨ р • r — тождественные.
Символ интерпретируется как противоположное состояние переключателя, т.е. если р = 1, то p = 0, а если переключатель р замкнут, то -p разомкнут. Так, формуле р v -p соответствует схема:

По этой цепи ток идет всегда, так как р ∨ р = 1, т.е. если переключатель р разомкнут, то переключатель -р замкнут, и наоборот. Лампочка горит постоянно. Можно упростить схему, убрав оба переключателя.
Алгебра логики располагает средствами, позволяющими найти наиболее простую схему (например, содержащую наименьшее число переключателей) по сравнению с данной, но выполняющую те же функции, что и исходная.
3. “Прекрасно приспособленная для описания комбинаторных явлений, эта теория получает многочисленные применения к исследованию операций, где ее нередко связывают с теорией структур”[69].
Алгебра логики применяется также в сетевом планировании и линейном программировании.
4. Алгебра логики применяется при установлении правильности или неправильности рассуждении. Пример рассуждения: “Если Иванов является участником этого преступления, то он знал потерпевшего. Иванов не знал потерпевшего, но знал его жену. Потерпевший знал Иванова. Следовательно, Иванов не является участником этого преступления.” Переведем рассуждение на язык алгебры логики. Обозначим символами простые суждения, входящие в рассуждение: “Иванов является участником этого преступления” (р), “Иванов знал потерпевшего” (q), “Иванов знал жену потерпевшего” (r), “потерпевший знал Иванова” (s). Затем переведем на язык алгебры логики посылки и заключение рассуждения. При этом вместо “если р, то q” напишем -p ∨ q. Союз “но” по смыслу соответствует союзу “и”.
Переводом посылок и заключения являются формулы:
-р ∨ q, -q • r, s и -p соответственно.
Формулы, переводящие посылки, последовательно соединим друг с другом символом “•”: ((p ∨ q) • (q • r)) • s.
Поставив над полученной формулой знак отрицания, присоединим к ней символом “∨” формулу, соответствующую заключению:

Полученная формула является переводом на язык символов исходного рассуждения. Если исходное рассуждение является правильным, то полученная формула равно 1.
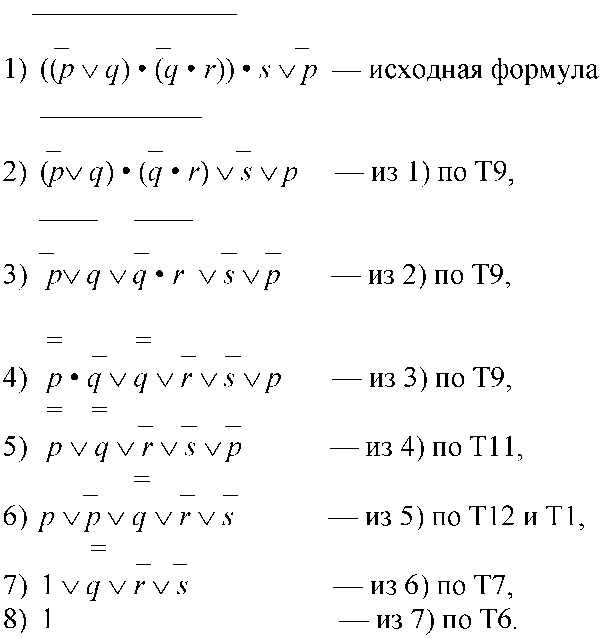
Анализируемое рассуждение является правильным.
ЗАКЛЮЧЕНИЕ
Студентам, прослушавшим курс логики и успешно сдавшим экзамен по этой дисциплине, мы советуем продолжить изучение логики, чтобы лучше освоить логические приемы и способы рассуждения, изложенные в этой книге, почерпнуть из литературных источников не описанные здесь логические средства, самим разработать по аналогии с имеющимися в логической науке способы борьбы с уловками и выявления алогизмов. Для этого целесообразно сохранить данный учебник или конспект лекций и при возможности приобретать другую учебную литературу по логике. Полезно, на наш взгляд, изучить книгу С. И. Поварнина “Искусство спора”. В ней излагаются разнообразные уловки, применяемые в процессе полемики. Знание этих уловок способствует более быстрому их выявлению.
Рекомендуется постоянно применять знание логики в процессе своей работы. Целесообразно также тактично обращать внимание товарищей по работе и всех, с кем приходится общаться, на случаи нелогичности их рассуждении и тем самым способствовать повышению логической культуры членов общества.
Применяя знание логики, необходимо выделять проблемные ситуации, для решения которых этих знаний недостает. Логических знаний, изложенных в данном учебнике, может недоставать по ряду причин.
Первая причина. Поскольку логика в настоящее время, в основном, изучается на юридических факультетах вузов, учебник ориентирован прежде всего на юристов. Профилизация большей частью заключается в отборе материала — излагаются логические средства, применяемые в указанной сфере человеческого познания. Чтобы расширить круг читателей, отобраны такие логические средства, которые применяются также в других гуманитарных науках, а также в естествознании и математике, однако в последних областях знания применяются еще и специфические способы рассуждения, приемы и методы, не излагаемые в данном учебнике. Например, при описании способов определения опускаются индуктивные и рекурсивные определения, широко используемые в математике; в главе “Умозаключение” не описывается рассуждение, называемое полной математической индукцией; нет таких разделов, как “логика квантовой механики’”, “виды объектов” (этот раздел особенно важен для химиков) и т.д.
Вторая причина заключается в том, что логика, как и многие другие науки, не завершила своего развития и отдельные ее разделы требуют дальнейшей разработки.
ОТВЕТЫ И РЕШЕНИЯ
Не нашли, что искали? Воспользуйтесь поиском: