Общие сведения и характеристики ИП

Ранее было дано определение измерительного преобразователя в соответствии с ГОСТ 16263-70. Но можно определить измерительный преобразователь (ИП) как техническое устройство, построенное на определенном физическом принципе действия, выполняющее одно частное измерительное преобразование.

Измерительное преобразование представляет собой отражение размера одной физической величины размером другой физической величины, функционально с ней связанной.

У каждого ИП устанавливается естественная входная величина, которая наилучшим образом воспринимается им на фоне помех, и естественная выходная величина, которая определяется подобным образом. Например, естественной входной величиной терморезистивного ИП является температура, а естественной выходной величиной - сопротивление.

Характеристики измерительных преобразователей можно в общем случае разделить на статические и динамические.

Статические характеристики определяют поведение ИП в таких условиях, когда входная величина не подвергается изменениям в процессе преобразования. К ним относятся функция преобразования, чувствительность, статическая погрешность и др.

Одной из основных характеристик ИП является функция (характеристика) преобразования - функциональная зависимость выходной величины от входной, которая может быть задана аналитической зависимостью, графиком или таблицей (например, функция преобразования платинового терморезистивного измерительного преобразователя ИП в диапазоне температур от 0 до +650 ⁰С может быть представлена в виде R_Т = R₀ (1 + АТ + ВТ²), где R₀ - сопротивление при 0 ⁰С; Т - температура, ⁰С; А и В - константы). Обычно стремятся получить линейную функцию преобразования.

В реальных условиях функция преобразования любого ИП не остается строго неизменной, так как она зависит от режима работы преобразователя, влияния внешних условий, условий нагрузки и ряда случайных факторов. Поэтому различают номинальную и реальную функции преобразования ИП.

Номинальная функция преобразования ИП - y_н = f_н(x) - функция, которую должен иметь ИП согласно государственным стандартам, ТУ или другим нормативным документам. Часто в качестве номинальной принимается средняя характеристика, полученная по результатам градуировки серии ИП. Эта характеристика (функция) указывается в паспорте на ИП.

При градуировке серии однотипных преобразователей функции преобразования каждого ИП могут отличаться от паспортной (номинальной), образуя полосу неопределенности.

Реальная функция преобразования y_р = f_р(x) - функция, которую имеет ИП в действительности.

Погрешность ИП - это разность между номинальной и реальной характеристикой преобразования ИП.

При определении погрешностей ИП имеются особенности:

1) входная и выходная величина могут иметь разную физическую природу; 2) часто отсутствует образцовый измерительный преобразователь, по которому можно проверить рабочий ИП.

Различают погрешность ИП по входу и погрешность по выходу. Разность значений реальной и номинальной функций преобразования при одном и том же значении входной величины определяет абсолютную погрешность ИП по выходу (рис. 5.1) Dy = y - y_н. Абсолютная погрешность измерительного преобразователя по входу определяется как Dх = х_н - х, где х - истинное значение входной величины; х_н - значение, определяемое по y_н = f_н(x), при значении выходной

У величины y_н, соответствующей ис-

y_н тинному значению. Выражения для

y_Р y_Р относительной d и приведенной g пог-

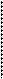
y_н решностей по выходу и входу могут

быть представлены в виде

х d_y = DY/Y; g_y = DY/(Y_max - Y_min);

х х_н d_Х = DХ/Х; g_x = DX/ (X_max - X_min).

Рис. 5.1 Если Y = SX, то d_y = d_х.

Иногда применяют термин точность СИ - качество СИ, отражающее близость к нулю его погрешностей.

Чувствительность преобразователя - это показатель относительного наклона характеристики преобразования. Для линейной функции чувствительность S = DY/DX (DY и DX - изменение выходной величины Y и вызвавшее его изменение входной величины Х). Для нелинейной функции преобразования Y = f(X) чувствительность может быть определена для данного значения входной величины S = dY/dX. Чувствительность ИП, как правило, именованная величина. Например, для медного терморезистивного ИП единица чувствительности - ом на кельвин (Ом/K). От чувствительности следует отличать порог чувствительности, который характеризует минимальное значение входной величины, уверенно обнаруживаемое с помощью данного ИП.

Динамические характеристики - характеристики инерционных СИ, которые определяют зависимость входного сигнала СИ от меняющихся во времени величин: параметров входного сигнала, внешних влияющих величин, нагрузки.

Динамические нагрузки определяют динамическую погрешность. Динамический учет всех факторов затруднен.

К динамическим характеристикам относятся: передаточная характеристика (передаточная функция), переходная характеристика, амплитудно-частотная характеристика (АЧХ), фазочастотная характеристика (ФЧХ).

Когда о законе изменения входной величины за время измерения могут быть высказаны достаточно обоснованные предположения и СИ является линейной системой, то СИ может быть охарактеризовано линейным дифференциальным уравнением с постоянными коэффициентами

a_n(dⁿy/dtⁿ) + a_n-1 (d^n-1 y/dt^n-1) + ^… + a₀y = x(t), (5.1)

где а_n, а_n-1 …, а₀ - постоянные коэффициенты.

При нулевых начальных условиях, т. е. t = 0; x = const, уравнение (5.1) в операторной форме можно записать в виде: (а_n pⁿ + а_n-1 p^n-1 + ^… + а₀)y = x(t).

Отношение изображений по Лапласу выходной величины Y(p) к входной X(p) - есть передаточная функция К(p) = Y(p)/X(p).

Зная K(p) средства измерения, можно определить его реакцию Y(t) на заданное изменение X(t) и определить динамическую погрешность D Y(t)

DY(t) =Y(t) - Y_СТ, (5.2)

где Y(t) - значение Y в момент t; Y_СТ - значение Y, заданное статической функцией преобразования.

Реакция Y(t) на воздействие в виде единичного скачка - это переходная характеристика (функция) h(t)

h(t) = L^-1[K(p)/p]. (5.3)

Комплексная чувствительность S(jw) - отношение комплексных амплитуд выходной и входной величин

S(jw)=Y(jw)/X(jw) = [b_m(jw) + ^… + b₀] / [a_n(jw) + ^… + a₀]. (5.4)

Выражение для S(jw) можно записать в виде

S(jw) = А + jB. (5.5)

АЧХ - зависимость модуля комплексной чувствительности от частоты. Из (5.5) получим

S(iw) = Ö A² + B². (5.6)

ФЧХ - зависимость аргумента комплексной чувствительности от частоты

j = arctg(B/A). (5.7)

Не нашли, что искали? Воспользуйтесь поиском: