Методы исключения систематических погрешностей

Результаты измерений, содержащие систематическую погрешность, относятся к неисправленным. При проведении измерений стремятся исключить, уменьшить или учесть влияние систематических погрешностей. Однако вначале их надо обнаружить.

Постоянные систематические погрешности можно обнаружить только путем сравнения результатов измерений с другими, полученными с использованием более точных методов и средств измерения. В ряде случаев такие погрешности можно устранить, используя специальные методы измерений.

Рассмотрим наиболее известные методы исключения (существенного уменьшения) постоянных систематических погрешностей.

Метод замещения обеспечивает наиболее полное решение задачи компенсации постоянной систематической погрешности. Суть метода состоит в такой замене измеряемой величины Хи известной величиной А, получаемой с помощью регулируемой меры, чтобы показание измерительного прибора сохранилось неизменным. Значение измеряемой величины считывается в этом случае по указателю меры.

При использовании данного метода погрешность неточного измерительного прибора устраняется, а погрешность измерения определяется только погрешностью самой меры и погрешностью отсчета измеряемой величины по указателю меры.

Пример. Измерялось сопротивление резистора Rx омметром малой точности. Результат измерения равен Х = Rx + Δс, где Х и Δс — соответственно показание омметра и систематическая погрешность измерения. Заменив Rx магазином сопротивлений и отрегулировав его так, чтобы сохранилось показание омметра, получим Х = Rм + Δс. Из приведенных двух выражений для х следует, что Rx = Rм.

Метод компенсации погрешности по знаку (метод двух отсчетов или изменения знака систематической погрешности) используется для устранения постоянной систематической погрешности, у которой в зависимости от условий измерения изменяется только знак. При этом методе выполняют два измерения, результаты которых должны быть равны

Х₁ = Хи + Δс

и

Х₂ = Хи - Δс.

где Хи — измеряемая величина. Среднее значение из полученных результатов

(Х₁ + Х₂)/2 = Хи

представляет собой окончательный результат измерения, не содержащий погрешности ±Δс. Данный метод часто используется при измерении экстремальных значений (максимума и нуля) неизвестной величины.

Пример. Измерить значение ЭДС потенциометром постоянного тока, который обладает паразитной термоЭДС.

Решение. Уравновесив потенциометр и выполнив первое измерение, получаем ЭДС U₁. Затем меняем полярность измеряемой ЭДС, а значит и направление тока в потенциометре. Снова проводим его уравновешивание и в результате второго измерения получаем значение U₂. Если термоЭДС дает погрешность ΔU и напряжение

U₁ = Ux + ΔU, то U₂ = Uх - ΔU.

Отсюда напряжение

Ux = (U₁ + U₂)/2.

Итак, систематическая погрешность, обусловленная действием термоЭДС потенциометра, устранена.

Метод противопоставления применяется в радиоизмерениях для уменьшения постоянных систематических погрешностей при сравнении измеряемой величины с известной величиной примерно равного значения, воспроизводимой соответствующей образцовой мерой. Этот метод является разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.

Пример. Измерить сопротивление резистора с помощью одинарного моста методом противопоставления.

Решение. Сначала измеряемое сопротивление Rx уравновешивают образцовой мерой — известным сопротивлением R1 включенным в плечо сравнения моста. При этом

Rx = R1R3/R4,

где R3, R4 — сопротивления плеч моста. Затем резисторы Rx и R1 меняют местами и вновь уравновешивают мост, регулируя сопротивление образцового резистора R1 = R'1 В этом случае

Rx = R'1R3/R4.

Из двух уравнений для Rx исключается отношение R3/R4. Тогда

.

Метод рандомизации (от англ. random — случайный, беспорядочный; в переводе на русский означает: перемешивание, создание беспорядка, хаоса) основан на принципе перевода систематических погрешностей в случайные.

Этот метод позволяет эффективно уменьшать постоянную систематическую погрешность (методическую и инструментальную) путем измерения некоторой величины рядом однотипных приборов с последующей оценкой результата измерений в виде математического ожидания (среднего арифметического значения) выполненного ряда наблюдений. В данном методе при обработке результатов измерений используются случайные изменения погрешности от прибора к прибору. Уменьшение систематической погрешности достигается и при изменении случайным образом методики и условий проведения измерений.

Поясним действие метода рандомизации простым примером. Пусть некоторая физическая величина измеряется n (число n достаточно велико) однотипными приборами, имеющими систематические погрешности одинакового происхождения. Для одного прибора эта погрешность — величина постоянная, но от прибора к прибору она изменяется случайным образом. Поэтому, если измерить неизвестную величину n приборами и затем вычислить математическое ожидание всех результатов, то значение погрешности существенно уменьшится (как и в случае усреднения случайной погрешности).

Метод введения поправок. Довольно часто систематические погрешности могут быть вычислены и исключены из результата измерения с помощью поправки. Поправка С — величина, одноименная с измеряемой Хи, которая вводится в результат измерения Х = Хи + Δс + С с целью исключения систематической погрешности Δс,.. В случае С = -Δс, систематическая погрешность полностью исключается из результата измерения. Поправки определяются экспериментально или путем специальных теоретических исследований и задаются в виде формул, таблиц или графиков.

Наиболее просто методом введения поправок исключают постоянные инструментальные систематические погрешности, которые обычно выявляют посредством поверки средства измерения.

Пример. При измерении напряжения в сети переменного тока показания вольтметра составили 218 В. В свидетельстве о поверке прибора указано, что на этой отметке его шкалы систематическая погрешность вольтметра составляет -2 В. С учетом поправки напряжение в сети равно 218 + 2 = 220 В.

Пример. Напряжение источника ЭДС Ux измерено вольтметром, сопротивление которого R_V = 5 кОм определено с погрешностью ± 0,5 %. Внутреннее сопротивление источника ЭДС Ri = 60 ±10 Ом. Показание вольтметра Uv = 12,50 В. Найти поправку, которую нужно внести, и показание прибора для определения действительного значения напряжения источника.

Решение. Показания вольтметра соответствуют падению напряжения на нем:

Относительная систематическая методическая погрешность, обусловленная ограниченным значением сопротивления R_V,

Поправка измерения напряжения равна абсолютной систематической погрешности, взятой с обратным знаком:

Δс= 12,50-0,012 = 0,15В.

Погрешность полученного значения поправки определяется погрешностью, с которой известно сопротивление Ri а это Δ = ± 10 Ом. Ее предельное значение составит

Δ_сRi = 10/60 = 0,167.

Погрешностью Δ_RV = 0,005 неточности оценки R_V можно пренебречь. Следовательно, погрешность определения поправки

Δ = ± 0,167 · 0,15 = 0,0251 ≈ 0,03 В.

Итак, в показания вольтметра необходимо ввести поправку:

ΔU= + 0,15 В.

Тогда исправленное значение

= 12,5 + 0,15 = 12,65 В.

Этот результат имеет определенную погрешность, в том числе неисключенный остаток систематической погрешности

Δ = ± 0,03 В

или

δ = ± 0,24 %

из-за потребления некоторой мощности вольтметром.

Ввод одной поправки позволяет исключить влияние только одной составляющей систематической погрешности. Для устранения всех составляющих, в результат измерения приходится вводить ряд поправок.

Рассмотрим далее некоторые методы, применяющиеся для обнаружения и уменьшения переменных и монотонно изменяющихся во времени систематических погрешностей.

Метод симметричных наблюдений весьма эффективен при выявлении и исключении погрешности, являющейся линейной функцией соответствующего аргумента (амплитуды, напряжения, времени, температуры и т. д.).

Предположим, что измеряется величина Хи, а результаты наблюдений Хi зависят от времени t. Для выявления характера изменения погрешности выполняют несколько наблюдений через равные промежутки времени Δt. Пусть выполнено пять наблюдений Х₁... Х₅ в моменты времени t₁... t₅. Далее вычисляют средние арифметические значения двух пар наблюдений

(Х₁ + Х₅)/2 и (Х₂ + Х₄)/2.

Наблюдения в этих парах проведены в моменты t₁, t₅ и t₂, t₄, симметричные относительно момента t3. При линейном характере изменения погрешности, полученные средние значения должны быть одинаковы. Убедившись в этом, результаты наблюдений можно записать в виде

Х_i = Хи + kt_i

где k — некоторая постоянная.

Пусть

Х1 = Хи + kt₁ и Х2 = Хи + kt₂.

Решение системы этих уравнений дает значение Хи свободное от переменной систематической погрешности:

Хи = (Х₂t₁ – X₁t₂)/(t₂ – t₁).

Подобным образом удается исключить погрешности, обусловленные, например, постепенным падением уровня напряжения источника питания (аккумулятора, батареи).

Метод анализа знаков неисправленных случайных погрешностей. Когда знаки неисправленных случайных погрешностей чередуются с некоторой закономерностью, имеет место переменная систематическая погрешность. Если у случайных погрешностей последовательность знаков «+» сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если же у случайных погрешностей группы знаков «+» и «-» чередуются, то имеет место периодическая систематическая погрешность.

Графический метод является наиболее простым для обнаружения переменной систематической погрешности в ряде результатов наблюдений. При этом методе рекомендуется построить график, на который нанесены результаты наблюдений в той последовательности, в какой они были получены. На графике через точки наблюдений проводят плавную линию, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.

В заключение отметим, что при измерениях всегда остаются неисключенные остатки систематических погрешностей (НСП).

Вопрос №4 Случайные погрешности (ошибки)

Случайными являются такие ошибки, которые меняются непредсказуемо от одного измерения к другому при определении одной и той же физической величины с помощью одной и той же измерительной системы при неизменных условиях. Обычно они обусловлены большим числом факторов, которые влияют на результат измерения независимо. Мы не можем скорректировать случайные ошибки, так как нам неизвестны их причины и следствием их являются случайные (непредсказуемые) колебания результата измерения.

Примерами случайных ошибок служат:

ошибки наблюдателя;

ошибки регулировки и настройки Ипри;

ошибки округления и т. д.

Все, о чем мы можем говорить, имея дело со случайными ошибками, это вероятность того, что ошибка будет той или иной величины. Теория вероятностей и мат. статистика дают возможность делать определенные утверждения при наличии случайных ошибок.

Можно считать, что как систематические, так и случайные ошибки вызываются сигналом помехи, который накладывается на истинный сигнал при его измерении. Флюктуация помехи вызывает случайную ошибку, а постоянный сигнал помехи является причиной систематической погрешности. К сожалению, постоянный характер помехи делает задачу обнаружения систематических ошибок более трудной.

Влияние случайных ошибок можно уменьшить, осуществляя измерения несколько раз и принимая в качестве конечного результата среднее значение результатов отдельных измерений. Возможно это тогда, когда измеряемая величина не изменяется на протяжении всех этих измерений и измерения выполняются быстро. Среднее значение результатов измерений имеет вид:

.

Среднее представляет собой лучшую возможную оценку значения постоянной ФВ по результатам измерений. Такой вывод можно сделать из того факта, что

Таким образом, сумма всех отклонений равна нулю. Кроме того, величина

минимальна.

Другими словами, минимальными являются рассеяние или разброс выборочных значений относительно среднего .

Мерой рассеяния в окрестности среднего является дисперсия (мера концентрированности распределения), равная по определению,

.

Обычно указывается квадратный корень из дисперсии; эта величина называется среднеквадратическим отклонением . Выборки , полученные в отдельных измерениях величины , при наличии случайный ошибок, можно представить на диаграмме в виде столбцов. Чтобы построить такую диаграмму, нам следует разбить диапазон всех возможных значений , включающий все выборки полученные в измерениях, на небольшие интервалы ширины , а затем отложить число выборок , попавших в эти небольшие интервалы 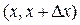, как функцию от (см рис.1). Обычно размер мелких интервалов выбирается по правилу

.

Если , то лучшее определить значение по правилу Старджеса

.

Если ширину интервала 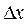выбрать слишком малой, то «огибающая» диаграммы будет сильно изрезанной. При слишком большом значении 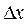«огибающая» оказывается квантованной слишком грубо, и форма распределения проступает не так явно.

Можно построить нормализованную диаграмму, откладывая 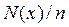, а не . Тогда по вертикали указывается относительное число измерений, результаты которых лежат в данном интервале. В этом случае можно утверждать, что теперь по оси ординат отложена вероятность попадания результата измерения в данный интервал. Кроме того, можно произвести нормализацию также и по ширине интервала , откладывая вместо 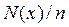. Диаграмму, получающуюся в результате нормализации, обычно называют гистограммой.

Рис.1 Гистограммы:

а. при правильном выборе ширины интервалов Δ х, на которые разбивается весь диапазон возможных значений х;

b. при слишком малых значениях Δ х;

c. при слишком больших значениях Δ х.

Если число выборок растет, а диапазон остается в ограниченных пределах, как это бывает на практике при измерении всех физических величин, то число интервалов, на которые разбивается этот диапазон, и число столбцов в гистограмме, увеличиваются, тогда как ширина одного интервала уменьшается. При огибающая гистограммы переходит в гладкую кривую. Такая (дважды) нормализованная гистограмма носит название плотности распределения вероятностей . По определению,

.

Это соотношение можно также записать в виде:

.

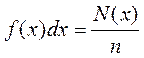Это означает, что есть вероятность того, что значение выборки попадает в интервал между и ; отсюда и следует название: плотность распределения вероятности. Из последнего равенства следует, что

.

Интеграл в этом выражении представляет собой сумму всех вероятностей . Он равен вероятности того, что очередная выборка попадет в первый интервал ширины , или во второй, или в третий и т.д. Так как результат измерения должен принадлежать одному из этих интервалов, сумма должна равняться 1. Последнее соотношение показывает, что единице равна площадь под плотностью распределения вероятностей (что и достигается, главным образом, путем двукратной нормализации). Зная плотность распределения вероятностей, легко найти вероятность того, что результат очередного измерения окажется меньше определенного значения а (см. рис.2). Обозначая эту вероятность , получим

Эта величина в точности равна площади под слева от линии х = а (см. рис.2).

Рис.2 Плотность распределения вероятностей.

Точно так же при заданной плотности распределения можно найти среднее набора выборочных значений :

.

Эта величина получила название МОЖ случайной величины и равна сумме бесконечно большого числа произведений всех возможных значений случайной величины на бесконечно малые площади f(x)dx.

Дисперсию, как меру рассеяния случайной величины, можно представить в виде:

.

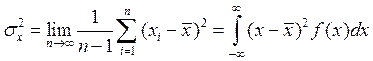Отметим ещё раз, что СКО – это квадратный корень из дисперсии:

СКО чаще всего используется для характеристики рассеяния (степени разбросанности) случайной величины и имеет ту же размерность, что и сама случайная величина.

Рис. 3. Кривые нормального распределения случайных погрешностей: 1—σ = 0,5а; 2—σ = 1а; 3—σ = 2а, где а — исходное значение

Рис. 4. Кривая нормального распределения случайных погрешностей и среднее квадратическое отклонение ± σ

На рис.3 указаны относительные значения среднего квадратического отклонения σ. Как видим, чем меньше σ, тем больше вероятность появления малых погрешностей и меньше вероятность появления больших погрешностей. Другими словами, тем больше сходимость результатов наблюдений.

Среднее квадратическое отклонение соответствует характерной точке кривой нормального распределения. Абсциссам +σ, -σ соответствуют точки перегиба кривой. Вероятность того, что случайные погрешности измерения не выйдут за пределы ±σ составляет 0,6826, приближенно 2/3. На рис.4 это соответствует попаданию в заштрихованную площадь, примерно в два раза большую, чем в незаштрихованную.

Если ошибки, содержащиеся в результатах измерений, обусловлены большим числом взаимно независимых событий, то можно доказать, что они распределены по вполне определенному закону: в этом случае распределение вероятностей является нормальным или гауссовым. Доказательство содержится в центральной предельной теореме теории вероятностей.

Нормальное распределение плотности вероятности характерно тем, что, согласно центральной предельной теореме теории вероятностей, такое распределение имеет сумма бесконечно большого числа бесконечно малых случайных возмущений с любыми распределениями. Применительно к измерениям это означает, что нормальное распределение случайных погрешностей возникает тогда, когда на результат измерения действует множество случайных возмущений, ни одно из которых не является преобладающим. Практически, суммарное воздействие даже сравнительно небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному.

Плотность вероятности нормального распределения имеет вид:

 

;

 

график такого распределения показан на рис.5. Вероятности того, что или х > + а, выражаются следующими интегралами, соответственно:

 

и

;

 

эти интегралы нельзя представить с помощью элементарных функций.

 

 

 

 

Рис.5 Нормальное или гауссово распределение

 

Примеры найденных численно приближенных значений этих интегралов представлены в табл.1.

 

«Вероятность того, что результат измерения, имеющий нормальное распределение со средним значением и СКО, лежит вне интервалов шириной 1 , 2 и 3 с центром в точке »

 

Табл.1

находится вне интервала	Вероятность
	0,32
	0,045
	0,0026

 

На рис.6 показан случай, когда результаты измерений содержат как случайные, так и систематические ошибки. Здесь случайные ошибки распределены по нормальному закону.

Истинное значение измеряемой величины равно а. Систематическая ошибка вызывает сдвиг среднего значения выборок, которое равно b. Полная ошибка (при верояности больших уклонений 0,14%) равна сумме систематической ошибки а-b и «максимальной случайной ошибки». Этой полной ошибкой определяется погрешность измерения. Неопределенность результата измерения является мера разброса между выборками, обусловленного только случайными ошибками. Строго говоря, неопределенность результата измерения задается интервалом, в пределах которого истинное значение измеряемой величины находится с заданной доверительной вероятностью.

 

 

Рис.6 Случайные и систематические ошибки

 

Оценка результата измерения. Задача состоит в том, чтобы по полученным экспериментальным путем результатам наблюдений, содержащим случайные погрешности, найти оценку истинного значения измеряемой величины — результат измерения. Будем полагать, что систематические погрешности в результатах наблюдений отсутствуют или исключены.

К оценкам, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности. Оценка называется состоятельной, если при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины.

Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой величины. В том случае, когда можно найти несколько несмещенных оценок, лучшей из них считается та, которая имеет наименьшую дисперсию. Чем меньше дисперсия оценки, тем более эффективной считают эту оценку.

Способы нахождения оценок результата зависят от вида функции распределения и от имеющихся соглашений по этому вопросу, регламентируемых в рамках законодательной метрологии. Общие соображения по выбору оценок заключаются в следующем.

Распределения погрешностей результатов наблюдений, как правило, являются симметричными относительно центра распределения, поэтому истинное значение измеряемой величины может быть определено как координата центра рассеивания Хц, т.е. центра симметрии распределения случайной погрешности (при условии, что систематическая погрешность исключена). Отсюда следует принятое в метрологии правило оценивания случайной погрешности в виде интервала, симметричного относительно результата измерения (Хц ± Δх). Координата Хц может быть найдена несколькими способами. Наиболее общим является определение центра симметрии из принципа симметрии вероятностей, т.е. нахождение такой точки на оси х, слева и справа от которой вероятности появления различных значений случайных погрешностей равны между собой и составляют P₁ = Р₂ = 0,5. Такое значение Хц называется медианой.

Координата Хц может быть определена и как центр тяжести распределения, т.е. как математическое ожидание случайной величины.

При ассиметричной кривой плотности распределения вероятностей оценкой центра распределения может служить абсцисса моды распределения, т.е. координата максимума плотности. Однако есть распределения, у которых не существует моды (например, равномерное), и распределения, у которых не существует математического ожидания.

В практике измерений встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным и равномерным распределением плотности вероятностей.

Учитывая многовариантность подходов к выбору оценок и в целях обеспечения единства измерений, правила обработки результатов наблюдений обычно регламентируются нормативно-техническими документами (стандартами, методическими указаниями, инструкциями). Так, в стандарте на методы обработки результатов прямых измерений с многократными наблюдениями указывается, что приведенные в нем методы обработки установлены для результатов наблюдений, принадлежащих нормальному распределению.

 

⇐ Предыдущая123Следующая ⇒

---

Не нашли, что искали? Воспользуйтесь поиском: