
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Занятие 2. Основные элементарные функции, их свойства и графики. Область определения функции. Четные и нечетные функции.
1. Действительные числа. Числа рациональные и иррациональные носят название действительных, или вещественных, чисел. Под абсолютной величиной действительного числа а понимается неотрицательное число | a |,определяемое условиями: | a | = a, если a ≥ 0, и | a | = − a, если а < 0. Для любых вещественных чисел а и b справедливо неравенство | a + b | ≤ | a | + | b |.
2. Определение функции. Если каждому значению переменной величины х, принадлежащему некоторой совокупности (множеству) E, соответствует одно и только одно конечное значение величины у, то у называется функцией (однозначной) от x,или зависимой переменной, определенной на множестве Е; x называется аргументом, или независимой переменной. То обстоятельство, что у есть функция от x,кратко выражают записью: y = f(x) и т. п.
Если каждому значению x,принадлежащему некоторому множеству Е,соответствует одно или несколько значений переменной величины у,то у называется многозначной функцией от x,определенной на множестве Е. В дальнейшем под словом «функция» мы будем понимать только однозначные функции, если явно не оговорено противное.
3. Область существования функции. Совокупность значений x,для которых данная функция определена, называется областью существования, или областью определения этой функции.
В простейших случаях область существования функции представляет собой: или отрезок (сегмент)[ а, b ],т. е. множество вещественных чисел x,удовлетворяющих неравенствам а ≤ х ≤ b; или промежуток (интервал)(а, b), т. е. множество вещественных чисел х, удовлетворяющих неравенствам а < x < b. Но возможна и более сложная структура области существования функции.
4. Обратные функции. Если уравнение y = f (x)может быть однозначно разрешено относительно переменного x,т. е. существует функция x = g (у)такая, что у = f [ g (у)],то функция x = g (y), или в стандартных обозначениях y = g (x), называется обратной по отношению к y = f (x). Очевидно, что g [ f (x)] = x, т. е. функции f (x)и g (x)являются взаимно обратными.
5. Сложные и неявные функции. Функция у от x,заданная цепью равенств y = f (u), где u = φ(x) и т.п., называется сложной, или функцией от функции.
Функция, заданная уравнением, не разрешенным относительно зависимой переменной, называется неявной. Например, уравнение х 3 + у 3 = 1 определяет у как неявную функцию от х.
6. Графическое изображение функции. Множество точек (x, у)плоскости ХОY, координаты которых связаны уравнением y = f (x), называется графиком данной функции.
Функция f (x), определенная в симметричной области − l < x < l,называется четной, если f (− x) = f (x), и нечетной, если f (−x) = − f (x).
Задачи:
Определить области существования функций:
11. а)  ; б)
; б)  . 15.
. 15.  . 17.
. 17. 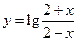 . 19.
. 19.  .
.
23. Выяснить, какие из данных функций являются четными и какие нечетными:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ;
;
д)  ;
;
Домашнее задание:
Определить области существования функций: 12.  . 13. а)
. 13. а)  ; б)
; б) 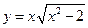 . 18.
. 18.  . 20.
. 20. 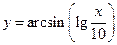 . 21.
. 21.  . 23(б, в, д)
. 23(б, в, д)
Ответы:
11. а)  ; б)
; б)  . 12.
. 12.  . 13. а)
. 13. а)  ; б)
; б)  . 15.
. 15. 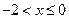 . 17.
. 17.  . 18.
. 18. 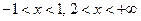 . 19.
. 19.  . 20.
. 20.  . 21.
. 21.  . 23. а) четная; б) нечетная; в) четная; г) нечетная; д) нечетная.
. 23. а) четная; б) нечетная; в) четная; г) нечетная; д) нечетная.
| <== предыдущая лекция | | | следующая лекция ==> |
| Задания к контрольной работе № 1 для студентов | | | Занятие 3. Элементарные методы построения графиков функций. |
Не нашли, что искали? Воспользуйтесь поиском: