Матрицы и операции над ними.

Прямоугольная таблица элементов некоторого множества , состоящая из строк и столбцов, называется матрицей порядка на (). Матрицы будем обозначать буквами а их элементы, находящиеся на пересечении строки и столбца через и т.д. Если , то матрица называется квадратной порядка . В общем виде матрица записывается следующим образом:

Коротко матрицу обозначают так:

Две матрицы и считают равными, если равны элементы, стоящие на одинаковых местах, т. е. если при всех 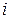и (при этом число строк (столбцов) матриц и должно быть одинаковым).

Матрицы можно складывать, умножать на число и друг на друга. Рассмотрим эти операции.

. Суммой двух матриц и одного и того же порядка называется матрица порядка , где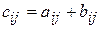

Пример 1.

. Произведением матрицы на число называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы на число :

Пример 2.

. Произведением матрицы , имеющей строк и столбцов, на матрицу , имеющую строк и столбцов, называется матрица
, имеющая m строк и n столбцов, у которой элемент равен сумме произведений элементов строки матрицы и столбца матрицы , т. е.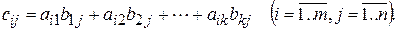

При этом число столбцов матрицы должно быть равно числу строк матрицы . В противном случае произведение не определено.

Пример 3.

.

Непосредственной проверкой можно убедиться в справедливости следующих свойств операций над матрицами:

1. - нулевая матрица (все элементы равны ).

2.

3.

4.

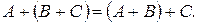
5.

6.

7.

Свойства 4 и 5 называются соответственно ассоциативностью и коммутативностью сложения матриц.

8.

9. .

10.

11.

Свойство 9 носит название ассоциативности умножения, а свойства 10 и 11– дистрибутивности умножения относительно сложения матриц. Эти свойства можно доказать, рассмотрев общий элемент матриц в левой и правой части этого равенства.

12.

Т. е. умножение матриц некоммутативно, например,

Совокупность элементов квадратной матрицы называется главной диагональю. Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные равны нулю, называется единичной матрицей и обозначается .

.

13. , для любой квадратной матрицы .

Если 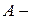матрица порядка , а 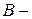матрица порядка , причём , то называют транспонированной матрицей по отношению к и обозначают через

14.

15.

Доказательство свойств 14 и 15 заключается в рассмотрении элемента в правой и левой частях этих равенств. □

Пусть 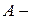квадратная матрица порядка . Она называется

- симметрической, если

- кососимметрической, если

Не нашли, что искали? Воспользуйтесь поиском: