
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Поле комплексных чисел.
На протяжении изучения предмета математики неоднократно происходит обогащение понятия числа. На первом этапе школьник, изучающий математику, сталкивается с натуральными числами  . С введением отрицательных чисел, появляется возможность рассмотрения системы целых чисел
. С введением отрицательных чисел, появляется возможность рассмотрения системы целых чисел  , состоящей из натуральных чисел, противоположных натуральным и нуля. Следующая, более широкая система рациональных чисел
, состоящей из натуральных чисел, противоположных натуральным и нуля. Следующая, более широкая система рациональных чисел  , состоящая из всех целых чисел и всех дробных, как положительных, так и отрицательных. Дальнейшее расширение понятия числа происходит тогда, когда в рассмотрение вводятся иррациональные числа. Система, состоящая из всех рациональных и всех иррациональных чисел, называется системой действительных (или вещественных) чисел
, состоящая из всех целых чисел и всех дробных, как положительных, так и отрицательных. Дальнейшее расширение понятия числа происходит тогда, когда в рассмотрение вводятся иррациональные числа. Система, состоящая из всех рациональных и всех иррациональных чисел, называется системой действительных (или вещественных) чисел  . Комплексные числа вводятся в связи со следующей задачей: нужно расширить систему действительных чисел до такой системы, в которой каждое квадратное уравнение (в частности уравнение
. Комплексные числа вводятся в связи со следующей задачей: нужно расширить систему действительных чисел до такой системы, в которой каждое квадратное уравнение (в частности уравнение 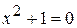 ) обладало бы корнем.
) обладало бы корнем.
В качестве материала для построения новой системы чисел возьмём точки плоскости  , каждая из которых однозначно определяется упорядоченной парой действительных чисел. Введём операции сложения и умножения для таких элементов следующим образом:
, каждая из которых однозначно определяется упорядоченной парой действительных чисел. Введём операции сложения и умножения для таких элементов следующим образом:
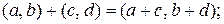
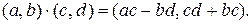
Покажем, что множество  с введёнными операциями сложения и умножения образует поле. Очевидно, сложение и умножение являются коммутативными операциями, а сложение, кроме того, ассоциативно. Нейтральным элементом по сложению является пара
с введёнными операциями сложения и умножения образует поле. Очевидно, сложение и умножение являются коммутативными операциями, а сложение, кроме того, ассоциативно. Нейтральным элементом по сложению является пара  , по умножению -
, по умножению -  . Для пары
. Для пары  противоположна пара
противоположна пара  . В качестве упражнения читателю предлагается доказать ассоциативность умножения и дистрибутивность умножения относительно сложения. Осталось показать, что для каждого ненулевого элемента существует обратный. Для этого решим уравнение
. В качестве упражнения читателю предлагается доказать ассоциативность умножения и дистрибутивность умножения относительно сложения. Осталось показать, что для каждого ненулевого элемента существует обратный. Для этого решим уравнение  относительно
относительно 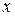 и
и  . Оно сводится к решению системы двух линейных уравнений с двумя неизвестными:
. Оно сводится к решению системы двух линейных уравнений с двумя неизвестными:
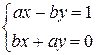
Данная система совместна для  и имеет единственное решение
и имеет единственное решение  , т. е.
, т. е.  .
.
Итак, система  является полем и называется системой комплексных чисел.
является полем и называется системой комплексных чисел.
Покажем теперь, что система комплексных чисел является расширением системы действительных чисел. Для этой цели рассмотрим точки, лежащие на оси абсцисс, т. е. точки вида  . Для них справедливо
. Для них справедливо
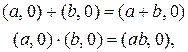
т. е. они складываются и перемножаются так же, как соответствующие действительные числа. Это позволяет нам в дальнейшем не различать точку  и действительное число
и действительное число 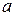 .
.
Вернёмся к уравнению 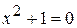 . Во множестве комплексных чисел его решением будет, например, точка
. Во множестве комплексных чисел его решением будет, например, точка  . Действительно,
. Действительно,  . Условимся обозначать эту точку буквой
. Условимся обозначать эту точку буквой 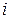 , так что
, так что  . Будем называть комплексное число
. Будем называть комплексное число 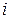 мнимой единицей. Имеем,
мнимой единицей. Имеем, 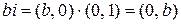 . Таким образом,
. Таким образом,  . Следовательно, любое комплексное число можно представить в виде
. Следовательно, любое комплексное число можно представить в виде  , где
, где 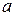 называется действительной частью комплексного числа, а
называется действительной частью комплексного числа, а  мнимой частью. Плоскость, точки которой отождествлены с комплексными числами, будем называть комплексной плоскостью. Ось абсцисс этой плоскости называется действительной осью, а ось ординат - мнимой осью.
мнимой частью. Плоскость, точки которой отождествлены с комплексными числами, будем называть комплексной плоскостью. Ось абсцисс этой плоскости называется действительной осью, а ось ординат - мнимой осью.
Положение точки  на плоскости однозначно задаётся парой действительных чисел
на плоскости однозначно задаётся парой действительных чисел 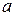 и
и 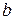 . Однако, её положение также вполне определяется с помощью полярных координат, т. е. расстоянием
. Однако, её положение также вполне определяется с помощью полярных координат, т. е. расстоянием  от точки до начала координат и углом
от точки до начала координат и углом  между положительным направлением оси абсцисс и направлением из начала координат на эту точку. Число
между положительным направлением оси абсцисс и направлением из начала координат на эту точку. Число  называется абсолютной величиной или модулем комплексного числа, а число
называется абсолютной величиной или модулем комплексного числа, а число  аргументом. Очевидно, что абсолютная величина неотрицательна, а аргумент определён с точностью до слагаемых, кратных
аргументом. Очевидно, что абсолютная величина неотрицательна, а аргумент определён с точностью до слагаемых, кратных  .
.
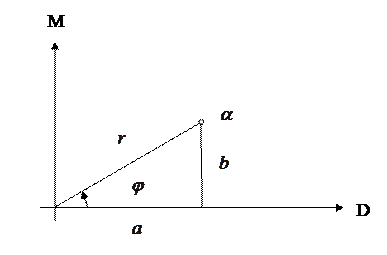
Между декартовыми и полярными координатами существует следующая связь, справедливая при любом расположении точек на плоскости:
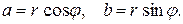
Для произвольного комплексного числа  имеем:
имеем:
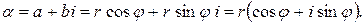
Эта запись числа  называется его тригонометрической формой. Абсолютная величина
называется его тригонометрической формой. Абсолютная величина  находится по формуле
находится по формуле  . Аргумент
. Аргумент  может быть найден из системы уравнений:
может быть найден из системы уравнений:
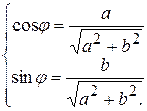
Пример 7. Найти тригонометрическую форму числа  .
.
 Решение. Здесь
Решение. Здесь  ,
,  . Тогда
. Тогда 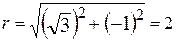 .
.
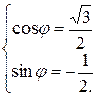
Решая систему, получаем  . Таким образом
. Таким образом
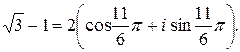
Пусть комплексные числа  и
и 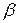 заданы в тригонометрической форме:
заданы в тригонометрической форме: 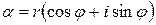 ,
,  . Перемножим эти числа:
. Перемножим эти числа:
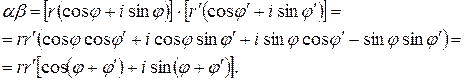
Таким образом, модуль произведения комплексных чисел равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей. Аналогичное правило имеет место и для частного. Если  , то:
, то:
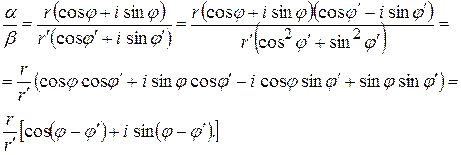
Следовательно, модуль частного двух комплексных чисел равен модулю делимого, делённому на модуль делителя, а аргумент частного получается вычитанием аргумента делителя из аргумента делимого.
Следствием из формулы умножения комплексных чисел является формула Муавра:

Пусть, теперь, нужно извлечь корень  степени из числа
степени из числа 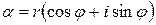 . Предположим, что это сделать можно и что в результате получается число
. Предположим, что это сделать можно и что в результате получается число  , т. е.
, т. е.
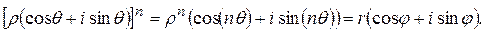
Тогда  - однозначно определённое положительное значение корня
- однозначно определённое положительное значение корня  ой степени из неотрицательного действительного числа
ой степени из неотрицательного действительного числа  . А аргументы
. А аргументы  и
и  могут отличаться на слагаемое, кратное
могут отличаться на слагаемое, кратное  , т. е.
, т. е.  , где
, где  целое число. Откуда
целое число. Откуда 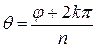 . Таким образом, окончательно имеем:
. Таким образом, окончательно имеем:
 .
.
Давая  различные значения, мы не всегда будем получать различные значения искомого корня. Действительно, при
различные значения, мы не всегда будем получать различные значения искомого корня. Действительно, при
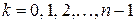
получим  значений корня, которые все будут различными, так как увеличение
значений корня, которые все будут различными, так как увеличение  на единицу влечёт за собой увеличение аргумента на
на единицу влечёт за собой увеличение аргумента на  . Для произвольного
. Для произвольного  имеем
имеем  , следовательно
, следовательно
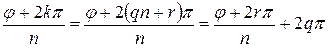 ,
,
т. е. значение аргумента при этом  отличается от значения аргумента при
отличается от значения аргумента при 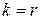 на число, кратное
на число, кратное  . Следовательно, значение корня при произвольном
. Следовательно, значение корня при произвольном  такое же, как при значении
такое же, как при значении  , равном
, равном  , где
, где  .
.
Таким образом, извлечение корня  ой степени из комплексного числа
ой степени из комплексного числа  всегда возможно и даёт
всегда возможно и даёт  различных значений. Все значения корня
различных значений. Все значения корня  ой степени расположены на окружности радиуса
ой степени расположены на окружности радиуса 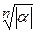 с центром в нуле и делят эту окружность на
с центром в нуле и делят эту окружность на  равных частей.
равных частей.
Пример 8. Вычислить  .
.
Решение. 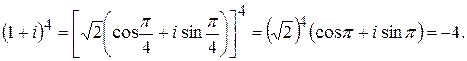
Пример 9. Вычислить  .
.
Решение. Найдём тригонометрическую форму числа 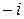 :
:
 .
.
Тогда 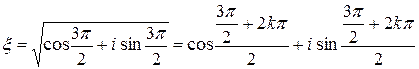 .
.
При  имеем:
имеем: 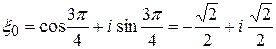 .
.
При  :
:  .
.
Пример 10. Вычислить  .
.
Решение. В тригонометрической форме  .
.
 .
.
 :
:  ;
;
 :
: 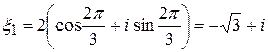 ;
;
 :
:  .
.
Поля вычетов.
Пусть  множество всех остатков от деления целых чисел на натуральное число
множество всех остатков от деления целых чисел на натуральное число  , т. е.
, т. е.  . Суммой (произведением) двух элементов будем считать остаток от деления этой суммы (произведения) на число
. Суммой (произведением) двух элементов будем считать остаток от деления этой суммы (произведения) на число  . Рассмотрим полученную структуру
. Рассмотрим полученную структуру 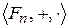 .
.
ТЕОРЕМА 6. Если  составное, то
составное, то  не является полем.
не является полем.
ДОКАЗАТЕЛЬСТВО. Пусть  составное, т. е.
составное, т. е.  , где
, где 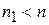 и
и  . Тогда по модулю
. Тогда по модулю  получаем
получаем  , но
, но  и
и  . Так как в поле такого быть не может (теорема 5), то при составном
. Так как в поле такого быть не может (теорема 5), то при составном  остатки с операциями по модулю
остатки с операциями по модулю  не образуют поля. □
не образуют поля. □
Покажем теперь, что в случае простого  ,
,  является полем. Вначале заметим следующее. Пусть
является полем. Вначале заметим следующее. Пусть 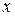 и
и  — два целых числа,
— два целых числа,  - остатки от деления их на
- остатки от деления их на  , т. е.
, т. е.  и
и  . Тогда
. Тогда  и
и  , откуда получаем, что числа
, откуда получаем, что числа  и
и 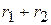 , а также числа
, а также числа  и
и  дают при делении на
дают при делении на  одинаковые остатки. Другими словами, мы получим одинаковый результат, если сначала возьмем остатки от деления
одинаковые остатки. Другими словами, мы получим одинаковый результат, если сначала возьмем остатки от деления 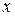 и
и  на
на  и потом сложим (или умножим) их по модулю
и потом сложим (или умножим) их по модулю  , или, если мы сначала сложим (или умножим)
, или, если мы сначала сложим (или умножим) 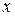 и
и  , как обычные натуральные числа, а затем возьмем остаток от деления полученного числа на
, как обычные натуральные числа, а затем возьмем остаток от деления полученного числа на  . Таким образом, при вычислении некоторого выражения с операциями по модулю
. Таким образом, при вычислении некоторого выражения с операциями по модулю  можно не брать остаток от деления на
можно не брать остаток от деления на  после каждой операции, а произвести вычисления сначала как с обычными натуральными числами и обычными операциями и только в конце взять остаток от деления полученного числа на
после каждой операции, а произвести вычисления сначала как с обычными натуральными числами и обычными операциями и только в конце взять остаток от деления полученного числа на  . Это позволяет утверждать, что операции сложения и умножения ассоциативны и коммутативны, а также справедлива дистрибутивность умножения относительно сложения.
. Это позволяет утверждать, что операции сложения и умножения ассоциативны и коммутативны, а также справедлива дистрибутивность умножения относительно сложения.
Нейтральным элементом по сложению является  , а единичным элементом по умножению -
, а единичным элементом по умножению -  . Остается показать, что при
. Остается показать, что при  простом у каждого остатка
простом у каждого остатка 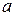 , отличного от
, отличного от  , есть обратный, т. е. что найдется остаток
, есть обратный, т. е. что найдется остаток 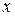 такой, что
такой, что  по модулю
по модулю  . Итак, пусть
. Итак, пусть  . Рассмотрим числа
. Рассмотрим числа
 (умножение обычное).
(умножение обычное).
Разность любых двух из этих чисел  не делится на
не делится на  , так как
, так как  простое, а
простое, а  и
и  . Таким образом, все эти
. Таким образом, все эти  чисел дают разные и, следовательно, всевозможные остатки при делении на
чисел дают разные и, следовательно, всевозможные остатки при делении на  . Значит, одно из этих чисел дает при делении на
. Значит, одно из этих чисел дает при делении на  остаток
остаток  , т. е.
, т. е.  по модулю
по модулю  для некоторого остатка
для некоторого остатка 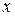 .
.
Таким образом, при  простом все свойства поля выполняются.
простом все свойства поля выполняются.
В качестве примера приведём таблицы сложения и умножения элементов поля вычетов по модулю 5.

| |||||

| |||||
По этим таблицам также можно получить разность и частное любых двух элементов.
Не нашли, что искали? Воспользуйтесь поиском: