Окружность на которой шаг равен шагу исходного контура, называют делительной.

Делительная прямая исходного контура и делительная окружность заготовки зубчатого колеса могут иметь различное взаимное расположение. Смещение обычно выражается в долях модуля xm, где x - коэффициент смещения исходного контура.

Возможны три случая относительного расположения делительной прямой и делительной окружности радиуса r.(рис.6.5).

1.Делительная прямая располагается на расстоянии от оси колеса, большем чем его радиус r. Зубчатые колеса, изготовленные при таком условии, называются положительными.

2.Делительная прямая касается делительной окружности, х=0. Зубчатые колеса, получаемые при этом, называются нулевые.

3.Делительная прямая располагается на расстоянии от оси колеса, меньшем, чем его радиус r. Зубчатые колеса, получаемые при этом называются отрицательные.

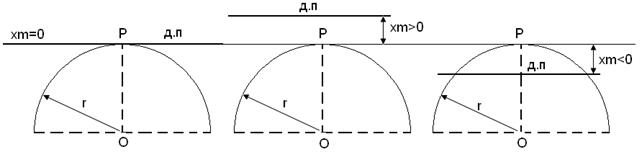
Рис.6.5

Форма зубьев колес, нарезанных с различным смещением инструмента, показана на рис.6.6. Смещение изменяет форму зуба. Так, положительное смещение приводит к утолщению зуба у основания и уменьшению кривизны профиля. Такое изменение формы способствует повышению его прочности. Выбор того или иного смещения зависит от назначения зубчатой передачи, условий, в которых она работает, нагрузок на элементы зубчатой передачи и т.д.

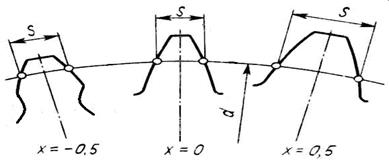
Рис.6.6

В зацепление можно вводить зубчатые колеса, изготовленные с различным сдвигом режущего инструмента. Возможны следующие сочетания:

åX= X₁ + Х₂ > 0 - положительное зацепление;

åX= X₁ + Х₂ = 0 - нулевое зацепление;

åX= X₁ + Х₂ < О - отрицательное зацепление.

Не нашли, что искали? Воспользуйтесь поиском: