Электрические сопротивления собственно свариваемых деталей

Электрическое сопротивление собственно деталей — это сопротивление, которое определенным образом распределено в объеме деталей, расположенном между сжимающими их электродами.

Величину электрического сопротивления собственно детали r_Д в большинстве случаев определяют по методике А. С. Гельмана. Еще в 40-х годах 20-го в. им была теоретически определено распределение потенциалов в свариваемых деталях путем решения методом конечных разностей дифференциального уравнения, описывающего электрическое поле

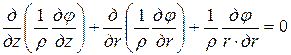, (2.15)

где φ — потенциал в рассматриваемой точке; z и r — цилиндрические координаты пространства.

Решением этого уравнения с граничными условиями, отражающими особенности протекания электрического тока при точечной сварке на участке электрод–детали–электрод, им определена топография растекания линий тока в деталях до диаметра d_j (см. рис 2.18) при различных условиях сварки и разработана инженерная методика расчета электрического сопротивления r_Д собственно свариваемых деталей [16, 85, 155]:

, (2.16)

где: А_Г — коэффициент (рис.2.20), учитывающий уменьшение сопротивления детали r_Д относительно сопротивления цилиндра r_Ц, высотой s и диаметром d_К, которое происходит из-за растекания линий тока до диаметра d_j; ρ_Т — удельное электрическое сопротивление металла деталей; k_Р — коэффициент, учитывающий неравномерность нагрева деталей.

Следует отметить поразительную, для того времени и тех вычислительных средств (расчетов на арифмометрах), точность решения
А. С. Гельмана. В 70-х годах многие исследователи подобные задачи начали решать на ЭВМ. Естественно, что некоторые из них пытались уточнить решение А. С. Гельмана. Как это ни удивительно, но значения коэффициента А_Г (сейчас его так и называют — «коэффициент Гельмана»), полученные с помощью арифмометра [155] и ЭВМ, например, в работе [157], практически совпадают.

При решении этой же задачи растекание линий тока в деталях
К. А. Кочергин моделирует их токопроводящее сечение в виде двух усеченных конусов, вершинами обращённых к контактам (показаны штриховыми линиями на рис 2.18). Это же сопротивление деталей r_Д он рассматривает как сумму сопротивлений конусов и сопротивлений за счет искривления линий тока в близи контакта (уменьшения площади токопроводящего сечения). В результате такого решения [4, 13] величину r_Д им предложено определять по следующей зависимости:

, (2.17)

где φ — коэффициент, который представляет собой отношение электрического сопротивления конусов к сопротивлению цилиндра диаметром d_К и высотой, равной толщине деталей s.

При расчетах r_Д по зависимости (2.17) значение диметра d_j, до которого происходит растекание линий тока в деталях, т. е. диаметра основания конуса, определяется через тот же коэффициент А.С. Гельмана А_Г:

.

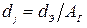Таким образом, по существу эти методики расчета электрического сопротивления свариваемых деталей представляют собой одно и то же решение данной задачи. Они различаются только тем, что в зависимости (2.16) рассчитывается уменьшение r_Д, которое происходит из-за растекания линий тока в деталях до диаметра d_j, относительно сопротивления цилиндра, диаметром d_К, а в зависимости (2.17) — наоборот, рассчитывается увеличение r_Д относительно сопротивления цилиндра, диаметром d_j, которое происходит из-за сужения линий тока у контактов до диаметра d_К.

Преимущественное применение в практике расчетов зависимости (2.16) объясняется, во-первых, тем, что диаметр контакта d_К, в отличие от d_j, в процессе сварки можно легко измерить, а во-вторых, по-видимому, и тем, что методика А.С. Гельмана предложена намного раньше.

Не нашли, что искали? Воспользуйтесь поиском: