Определение натуральной величины отрезка прямой

Определение натуральной величины отрезка прямой общего положения и углов наклона ее к плоскостям проекций производится способом прямоугольного треугольника.

Как видно из рисунка 1.3.7, длину отрезка прямой АВ можно определить из прямоугольного треугольника АВ¹В₁, в котором: катет АВ₁=А₁В₁ (проекция отрезка АВ на плоскость П₁), а катет ВВ¹= – разности расстояний точек А и В

от плоскости П₁ (Δz=z_А-z_В). Угол φ в этом же треугольнике определяет угол наклона отрезка прямой АВ к плоскости П₁.

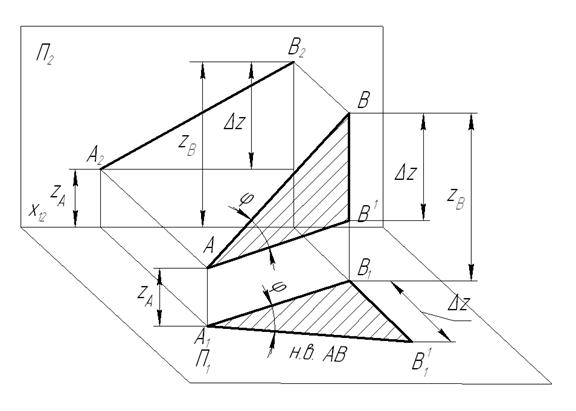
Рисунок 1.3.7 – Определение натуральной величины отрезка способом прямоугольного треугольника

Чтобы понять принцип нахождения натуральной величины отрезка прямой и угла наклона его к плоскости проекций на комплексном чертеже, совместим треугольник АВ¹В₁ с горизонтальной плоскостью проекций. Для этого примем горизонтальную проекцию А₁В₁ за один из катетов этого треугольника. Через точку В₁ проведем на плоскости П₁ прямую, перпендикулярную к А₁В₁, и отложим на ней от точки В₁ отрезок ВВ¹=Δz, равный длине второго катета. Соединив точки А₁ и В₁¹ прямой, получим прямоугольный треугольник А₁В₁В₁¹ = АВ¹В, так как А₁В₁=АВ¹, В₁В₁¹=ВВ¹ и угол А₁В₁В₁¹=90º.

В соответствии с рисунком 1.3.8 выполняются построения по нахождению натуральной величины отрезка АВ и его угла наклона к горизонтальной плоскости проекций на комплексном чертеже.

Рисунок 1.3.8 – Определение натуральной величины отрезка способом прямоугольного треугольника на комплексном чертеже

Аналогичные построения можно выполнить, использовав фронтальную проекцию А₂В₂ в качестве одного из катетов треугольника, тогда другой катет - Δy будет равен разности расстояний точек А и В от плоскости П₂. Гипотенуза треугольника будет также равна АВ, а угол ψ определит угол наклона отрезка прямой АВ к плоскости П₂.

Выводы:

- натуральная величина прямой общего положения равна гипотенузе прямоугольного треугольника, одним катетом которого будет являться проекция отрезка на любую плоскость проекций, а другим – разность расстояния концов отрезка от той же плоскости;

- угол между катетом-проекций и гипотенузой равен натуральной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения.

Не нашли, что искали? Воспользуйтесь поиском: