Т а б л и ц а 2 - Интервальный статистический ряд

	[ t0, t1)	[ t1, t2)	…	[ tk-1, tk ]
			…

здесь .

Перечень наблюдаемых значений СВ X (или интервалов наблюдаемых значений) и соответствующих им относительных частот называется статистическим законом распределения.

На втором этапе исследования находят точечные и интервальные оценки числовых характеристик ГС, а также оценки параметров её функции распределения.

Точечной оценкой некоторого неизвестного параметра называется функция от выборки (статистика) такая, что выполняется приближенное равенство

.

Приведём примеры точечных оценок. Точечной оценкой величины ГС является средняя величина выборки (обозначается , А₁ или ).

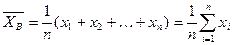. (1)

Точечными оценками для являются также мода, медиана и т.д. (см. / 2,3/).

Точечными оценками для генеральной дисперсии D_Г, характеризующей разброс ГС вокруг математического ожидания (), являются дисперсия выборки, обозначаемая S ² или D_В, и несмещенная выборочная дисперсия S₁².

(2)

(3)

Величины S ² и S ₁² существенно различаются только при малых n (n < 30), далее они практически совпадают.

Для характеристики рассеивания ГС вокруг своего математического ожидания рассматривают наряду с D_Г среднее квадратическое отклонение .

В качестве оценок для 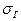применяют величины , , размах, коэффициент вариации и ряд других, /2,3/.

Среди оценок, характеризующих один и тот же параметр генеральной совокупности, выбирают “лучшие” в некотором смысле. Для того чтобы точечная оценка неизвестного параметра была “хорошей” прежде всего с точки зрения точности и надёжности, желательно, чтобы её значения , найденные по разным выборкам из одной и той же ГС, были тесно сконцентрированы вокруг оцениваемого параметра .

Желательно, также, чтобы точность оценки при увеличении объёма выборки увеличивалась.

Оценка называется состоятельной, если при n ® она стремится по вероятности к оцениваемому параметру, т.е. " e > 0 .

Оценка называется несмещенной (оценкой без систематической ошибки) если её математическое ожидание равно оцениваемому параметру, т.е. если . Среди несмещенных оценок выделяется эффективная оценка – оценка с наименьшей, среди всех оценок, дисперсией (при заданном объёме выборки).

Пример 5. Для оценки могут служить , мода и медиана. Все эти три оценки являются состоятельными и несмещенными. Наряду с этим является ещё и эффективной, поэтому при практических исследованиях применяется чаще, чем мода и медиана.

Для оценки D_Г применяются S ² и S ₁². Обе эти оценки состоятельны, а S ₁² кроме того и несмещенная (поэтому она и предпочтительнее).

Наряду с точечными оценками числовых характеристик ГС в статистике рассматриваются точечные оценки неизвестных параметров гипотетических функций распределения. Эти оценки находятся с помощью метода моментов или метода максимального правдоподобия /2, 3/.

Рассмотрим некоторые распределения и укажем оценки для их параметров.

1) Нормальное распределение.

Функция распределения имеет вид

.

Плотность распределения

.

Здесь два параметра распределения – и .

В качестве оценки для обычно берут . » = ,

– эффективная оценка. В качестве оценки для обычно берут S ₁

.

График плотности нормального распределения имеет вид

Рисунок 1

2) Равномерное распределение.

где точечные оценки параметров равномерного распределения.

График плотности равномерного распределения имеет вид

f(x)

0 a b x

Рисунок 2

3) Показательное распределение.

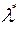– эффективная оценка параметра показательного распределения.

График плотности показательного распределения имеет вид

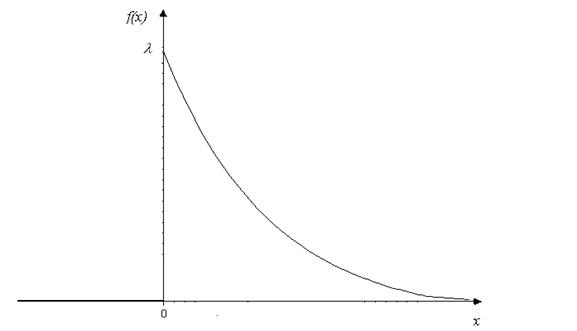
Рисунок 3

Наряду с точечными оценками в математической статистике часто рассматривают интервальные оценки.

Точечной называют оценку, которая определяется для данной реализации выборки одним числом. Все оценки, рассмотренные выше, точечные. При выборках малого объёма точечные оценки могут значительно отличаться от оцениваемых параметров, т.е. приводить к грубым ошибкам. В связи с этим во многих случаях более удобно пользоваться интервальными оценками.

Пусть - точечная оценка параметра . Чем меньше модуль разности (расстояние) , тем лучше качество оценки, тем она точнее. Пусть выполняется неравенство

< d, где d > 0. (4)

Перепишем неравенство в виде

.

Получим, что неизвестный параметр лежит в интервале

. (5)

Интервальной называют оценку, которая определяется двумя числами - концами интервала. Величина d называется точностью оценки.

Необходимо четко понимать, что неравенство (4) выполняется не в обычном (детерминированном) смысле, а в вероятностном. Статистические методы не позволяют утверждать, что это неравенство выполняется всегда, можно только говорить о вероятности его выполнения.

Вероятность выполнения неравенства (4) называется доверительной вероятностью (надежностью).

Обычно вероятность оценки задается заранее, её выбирают близкой к единице. Наиболее часто полагают g = 0,95; 0,99; 0,999.

Доверительным интервалом называется интервал, накрывающий неизвестный параметр с заданной доверительной вероятностью g. В практических приложениях важную роль играет длина доверительного интервала, причем чем меньше эта длина, тем оценка точнее, но при этом уменьшается её надёжность (при заданном объеме выборки n). Поэтому если одновременно нужно улучшить и точность, и надежность, то надо увеличивать объем выборки или использовать более эффективную оценку.

Рассмотрим несколько примеров.

Пример 6. Доверительный интервал для математического ожидания СВ X, распределённой по нормальному закону, при известном имеет вид

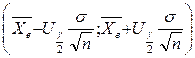, (6)

здесь находится из уравнения

,

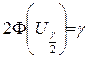где - функция Лапласа. Таблицы этой функции есть во многих учебниках и задачниках по теории вероятностей или математической статистике, например в руководстве /3/.

Пример7. Доверительный интервал для математического ожидания СВ Х, распределенной по нормальному закону, при неизвестном s_Г имеет вид

, (7)

здесь S ₁ - оценка среднеквадратичного отклонения, величина t_{γ, n- 1} при заданных n и γ находится по специальным таблицам, построенным с помощью статистики Стьюдента. В руководстве /3/ это таблица ПРИЛОЖЕНИЕ 3.

Пример 7. Доверительный интервал для оценки среднего квадратического отклонения σ_Γ СВ Х, распределенной по нормальному закону, имеет вид

(S₁(1-q); S₁(1+q)), (8)

где q = q_g,n находится по таблицам, построенным с помощью статистики χ ². В / 3 / это таблица ПРИЛОЖЕНИЕ 4.

На третьем этапе статистических исследований обычно выдвигают и проверяют гипотезы о виде и параметрах распределения. Для выдвижения подобных гипотез часто статистические ряды представляют графиками и диаграммами.

Наиболее распространенными графиками являются гистограмма, полигони эмпирическая функция распределения (кумулята).

Полигон и эмпирическая функция распределения применяются для изображения как дискретных, так и интервальных статистических рядов, гистограмма служит для изображения только интервальных рядов.

Существует два вида гистограмм – гистограмма частот и гистограмма относительных частот. Более удобно использовать гистограмму относительных частот – аналог графика плотности вероятностей.

Гистограммойотносительных частот называется ступенчатая фигура,состоящая из прямоугольников, основаниями которых служат частичныеинтервалы длинойh, а высоты равны отношению , где – относительные частоты на i-том интервале (см. таблицу 2 и рисунок 6).

Гистограмма частот отличается от гистограммы относительных частот только тем, что высоты прямоугольников равны .

В теории вероятностей функцию распределения СВ x определяют как вероятность того, что значение случайной величины x окажется меньше аргумента функции x

F(x) = P(x < x) (9)

Для дискретных СВ выражении (9) можно записать в виде

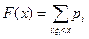
Следовательно, функция распределения может быть введена как сумма вероятностей значений СВ X.меньших аргумента функции x (лежащихна оси ОХ левее аргумента функции). В математической статистике аналогом вероятности является относительная частота, поэтому эмпирическую функцию распределения для дискретных СВ X естественно определить следующим образом

(10)

Аналогично вводится понятие эмпирической функции распределения для непрерывной СВ. Для этого сначала преобразовывают интервальный статистический ряд в сгруппированный статистический ряд,заменяякаждый i -ый интервал его серединой.

Затем для получившегося сгруппированного статистического ряда вводят F^*(x) по формуле (10).

После того, как по виду гистограммы, полигона или эмпирической функции распределения выдвинута гипотеза о виде распределения, приступают к ее проверке с помощью статистических критериев значимости. Чаще всего для проверки гипотезы о виде распределения применяют критерий Пирсона (критерий χ ²) или критерий Колмогорова (см. /3,4/). Проверяемую гипотезу называют основной и обозначают Н ₀. Наряду с основной рассматривают конкурирующую или альтернативную гипотезу, ее обозначают Н ₁ или Н _а. Если в процессе статистического доказательства основную гипотезу отвергают, то принимается альтернативная. При статистической проверке гипотез возникают ошибки первого и второго рода. Их появление связано с тем, что выборка недостаточно точно представляет генеральную совокупность (ГС), особенно это характерно для выборок малого объема. Может случиться так, что для ГС справедлива гипотеза Н ₀, но по результатам исследования мы ее отвергаем. В этом случае совершается ошибка 1^го рода. Если для ГС справедлива альтернативная гипотеза Н_а, а по реализации выборки (выбранной неудачно) мы принимаем гипотезу Н ₀, то совершается ошибка второго рода. Ошибки 1^го и 2^го рода тесно связаны между собой, при уменьшении вероятности ошибки 1^го рода возрастает вероятность ошибки 2^го рода и наоборот. Подробно динамику ошибок 1^го и 2^го рода можно посмотреть в /1, 5/. Одновременно уменьшение вероятностей ошибок 1^го и 2^го родов можно обеспечить увеличением объема выборки. К сожалению, избавиться от них вообще невозможно, за единственным исключением. Оставим этот вопрос об исключении на самостоятельную работу. Вероятность ошибки первого рода называется уровнем значимости и обозначается a. При практических исследованиях величинуa. берут близкой к нулю. Обычно ее выбирают равной 0,05, 0,01, 0,001 и т.д., в зависимости от ожидаемых суммарных последствий ошибок первого и второго рода.

Рассмотрим подробно алгоритм применения критерия χ ².

Пусть СВ Х имеет гипотетическую функцию распределения F(x). Пусть из ГС извлечена выборка объема n. Требуется на основе имеющейся информации проверить гипотезу о том, что F(x) хорошо представляет данную выборку. Разобьем весь диапазон полученных результатов на k частичных интервалов равной длины, и пусть в i -том частичном интервале оказалось m _i значений выборки (Sm_i = n). Составим интервальный статистический ряд распределения частот

Т а б л и ц а 3 - Интервальный статистический ряд распределения частот

где t₀ = x _min, t_k = x _max.

Далее делаем следующее

1) На основании гипотетической функции F(x) найдем вероятности p_i попадания СВ Х в частичные интервалы (разряды) D_i.

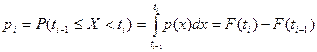
где i = 1,2,…, k.

2) Умножим подученные вероятности p_i на объем выборки n и получим теоретические частоты np_i, т.е. частоты, которые следует ожидать, если нулевая гипотеза справедлива.

3) Оценим отклонение теоретических частот от эмпирических с помощью статистики c² (предложенной Пирсоном)

. (11)

Чем ближе значение c²_набл к нулю, тем вероятнее, что гипотеза Н ₀ справедлива.

4) По таблицекритических точек распределения c² при заданном уровне значимости a и числе степеней свободы n находим c²_табл.

Число степеней свободы n определяется формулой n = k – r – 1, где k - число интервалов, r - число параметров гипотетической функции распределения F(x).

5) Если c²_набл < c²_табл, то гипотеза H ₀ (основная гипотеза) принимается, если c²_набл ³ c²_табл, то нулевую гипотезу отвергают.

Заметим, что объем выборки должен быть достаточно велик (n ³ 50), каждый разряд должен содержатьне менее 5-8 значений выборки.

Алгоритм проверки гипотезы Н ₀ с помощью других статистических критериев аналогичен, только вместо (11) применяют другие статистики.

Не нашли, что искали? Воспользуйтесь поиском: